Question
Question: The deflection in a galvanometer falls from \(50\) divisions to \(20\) divisions, when a \(12\Omega ...
The deflection in a galvanometer falls from 50 divisions to 20 divisions, when a 12Ω shunt is applied. The galvanometer resistance is
(A) 18Ω
(B) 24Ω
(C) 30Ω
(D) 36Ω
Solution
In order to solve this question, we will use the general formula of shunt resistance which is added to the galvanometer, and then using various parameters which are given in the question we will find the actual value of resistance of the given galvanometer.
Formula used:
To calculate the shunt resistance which is added to the galvanometer we use the general formula as,
S=(I−Ig)Ig.Rg
where,
S is the shunt resistance which is added to the galvanometer.
Ig is the current that passes through the galvanometer when shunt resistance is added.
I is the initial current passing through the galvanometer.
Rg is the actual resistance of the galvanometer.
Complete step by step answer:
If k is the figure of merit of the current of galvanometer then according to the question we have,
Ig=20k as the galvanometer drops to 20 divisions.
I=50k initial divisions.
S=12Ω shunt resistance.
Now, using the formula and putting the values of parameters we get, the magnitude and direction of current across galvanometer G and shunt resistance S is shown in diagram as
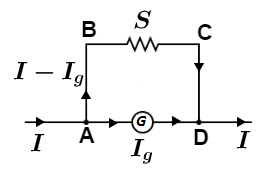
S=(I−Ig)Ig.Rg
12=(50k−20k)(20k)Rg
on solving we get,
12=3020Rg
or
Rg=18Ω
So, the value of actual resistance of the galvanometer is 18Ω
Hence, the correct option is (A) 18Ω.
Note: It should be remembered that, the figure of merit of any galvanometer is the amount of current required to pass through the galvanometer in order to produce a unit deflection in the galvanometer scale, and its denoted by k, so if n is the number of division and I is the current then current can simply be written as I=nk.
