Question

The data plotted on a graph of distance on the y-axis vs. time on the x-axis yields a linear graph. Identify which of the following options best describes the slope of the graph.
(A) $\dfrac{{\Delta d}}{{\Delta t}}$
(B) $(\Delta d)(\Delta t)$
(C) $\dfrac{{\Delta t}}{{\Delta d}}$
(D) $(\Delta d) + (\Delta t)$
(E) $(\Delta d) - (\Delta t)$

Answer 1

Hint
We need to draw a linear graph of distance on the y axis and time on the axis and take two points on it. Then we need to calculate the slope using its basic definition.
Formula Used: The formula used to solve this question is
$\tan \theta = \dfrac{{Height}}{{Base}}$

Complete step by step answer
As given in the question, the graph plotted between distance, $d$and time, $t$ is a linear graph. So we draw the graph according to the question.

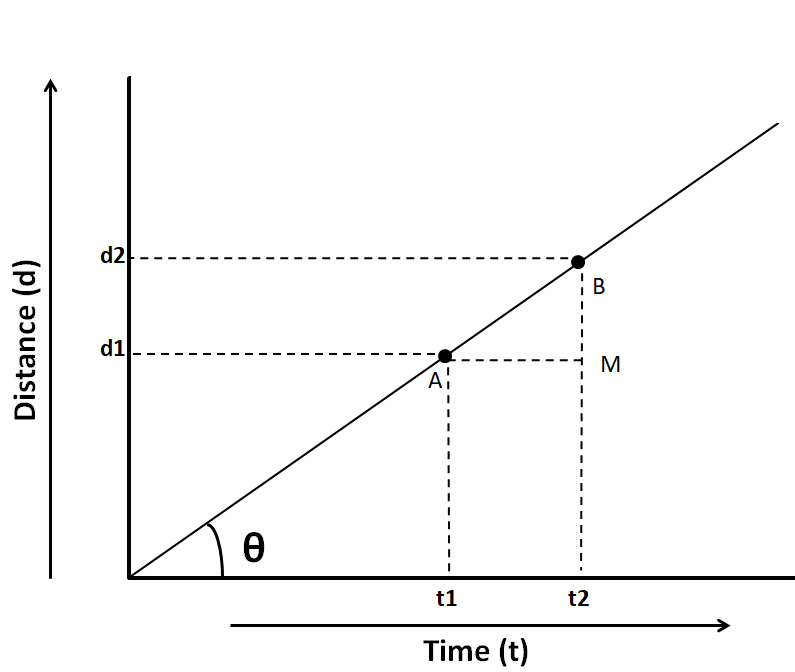
Let the graph make an angle of $\theta$ with the x-axis. As the graph is linear, so its slope is constant at each point on the graph. For calculating the slope, we take two points, A and B on the graph and calculate the slope from their corresponding coordinates. According to the definition, slope of a line is equal to the tangent of the angle made by that line with the x-axis, i.e.
Slope, $m = \tan \theta$
As $\tan \theta = \dfrac{{Height}}{{Base}}$
$\therefore m = \dfrac{{Height}}{{Base}} = \dfrac{{BM}}{{AM}}$
From the triangle AMB in the figure above,
$BM = d_2 - d_1$, ${\text{AM = t}}2 - t_1$
Substituting these in the above equation, we get
$m = \dfrac{{d_2 - d_1}}{{t_2 - t_1}}$
$\therefore m = \dfrac{{\Delta d}}{{\Delta t}}$
So, we have a slope equal to$\dfrac{{\Delta d}}{{\Delta t}}$.
Hence, the correct answer is option A, $\dfrac{{\Delta d}}{{\Delta t}}$/

Note
The graph in this question is plotted between distance and time. We know that the slope of such a graph indicates the velocity. So the unit of slope will be the same as the unit of velocity, i.e. $m/s$. From the options given, only A ($\dfrac{{\Delta d}}{{\Delta t}}$) has the unit of velocity. Thus, these types of questions can also be attempted through the knowledge of units and dimensions.