Question

The daily wages (in rupees) of 19 workers are 41, 21, 38, 27, 31, 45, 23, 26, 29, 30, 28, 25, 35, 42, 47, 53, 29, 31, 35. Find the median.

Answer 1

Here we arrange all the wages in ascending order or descending order so we either move higher up the scale or we move down the scale and then using the formula for median we choose the middlemost term from the observations.

• Median is the term that is exactly at the middle of the observations.
• If number of observations is odd then median is calculated by ${\left( {\dfrac{{n + 1}}{2}} \right)^{th}}term$
  If number of observations is even then, median is calculated by $\dfrac{{{{\left( {\dfrac{n}{2}} \right)}^{th}}term + {{\left( {\dfrac{n}{2} + 1} \right)}^{th}}term}}{2}$
• A number is odd if it can be expressed in the form $2n \pm 1$, example: $5 = 2 \times 2 + 1$ is an odd number.
• A number is even if it can be expressed in the form $2n$, example: $18 = 2 \times 9$ is an even number.

Complete step-by-step answer:
The daily wages are 41, 21, 38, 27, 31, 45, 23, 26, 29, 30, 28, 25, 35, 42, 47, 53, 29, 31, and 35
Total number of workers is 19
Since, these wages of workers are not in any ascending or descending order, therefore first we arrange them in ascending order (increasing order).
21, 23, 25, 26, 27, 28, 29, 29, 30, 31, 31, 35, 35, 38, 41, 42, 45, 47, 53
Now, the number of workers is 19 which is odd.
Therefore, using the formula for median when number of observations is odd
Median $= {\left( {\dfrac{{n + 1}}{2}} \right)^{th}}$term
Substituting the value of $n = 19$ in the formula
Median $= {\left( {\dfrac{{19 + 1}}{2}} \right)^{th}}$term
$= {\left( {\dfrac{{20}}{2}} \right)^{th}}$term
$= {10^{th}}$ term
Now take the ${10^{th}}$ term of the observations from left side or from right side.

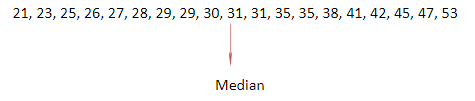
Therefore, ${10^{th}}$ term of the observations is 31.

So, the median of wages of 19 workers is 31.

Note: Students are likely to make mistakes in calculating the median when they have not arranged the observations in ascending or descending order. Usually students rush straight to the formula after counting the number of observations but that doesn’t work in both the cases.