Question
Question: The cylindrical tube of a spray pump has radius \(R\) , one end of which has \(n\) fine holes, each ...
The cylindrical tube of a spray pump has radius R , one end of which has n fine holes, each of radius r. If the speed of the liquid in the tube is V , the speed of the ejection of the liquid through the holes is:
A) nr2VR2
B) n3r2VR2
C) nrV2R
D) n2r2VR2
Solution
Use the continuity equation that compares the water through the cylindrical tube and also the holes in the cylindrical tube. Substitute the parameters of the area and the velocity in the formula, to obtain the relation for the speed of the water in the holes of the tube.
Useful formula:
The continuity equation is given by
A1v1=A2v2
Where A1 is the area of the cylindrical circumference, v1 is the speed of the liquid through the cylindrical tube, A2 is the area of the holes in the tube and the v2 is the velocity of the water through the small hole.
Complete step by step solution:
Thus the formula is taken,
A1v1=A2v2
Substitute the value of the area of the cylindrical circumference πR2 and the area of the small hole is considered as the πr2 in the above step.
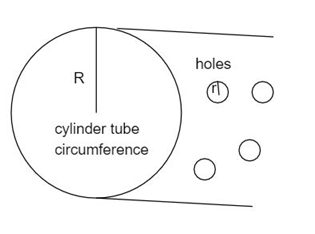
πR2V=πr2v
The above equation holds only for that of the one holes in the tube. While considering the equation of the n is the number of the holes in the tubes.
πR2V=nπr2v
The speed of the water through the holes in the tube is calculated as
v=nπr2πR2V
By simplification of the above step,
v=nr2VR2
Hence the value of the speed of the water in the holes, nr2VR2 .
Thus the option (A) is correct.
Note: The continuity equation deals with the conservation of the mass of the fluid and it states that the product of the area and the velocity is constant. That means the area and the velocity of one condition is equal to the product of the area and the velocity in the other condition.
