Solveeit Logo
Login

Question

Question: The curved line on the graph shows the motion of the car. What is the acceleration of the car at the...

The curved line on the graph shows the motion of the car. What is the acceleration of the car at the time of 4.0 s4.0\,s ?

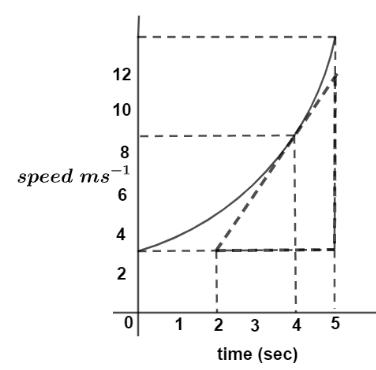
A. 0.33 m sec⁡−20.33\,m\,{\sec ^{ - 2}}
B. 0.44 m sec⁡−20.44\,m\,{\sec ^{ - 2}}
C. 2.3 m sec⁡−22.3\,m\,{\sec ^{ - 2}}
D. 3.0 m sec⁡−23.0\,m\,{\sec ^{ - 2}}

Explanation

Solution

In order to solve this question we need to understand distance, displacement, velocity, acceleration. Distance is defined as total path length travelled between initial and final points, displacement is defined as the shortest path length travelled between initial and final points, velocity is defined as the ratio of displacement and time, it is a vector quantity and the acceleration is defined as the ratio of velocity and time. So the area under the curve of the velocity time graph is displacement while the slope of the velocity time graph at any point is the acceleration at that point.

Complete step by step answer:
We know acceleration is defined graphically as the slope of the velocity time graph, so for acceleration at t=4sec⁡t = 4\sec we need to find a slope of the graph at this time. So we draw a perpendicular from t=4sec⁡t = 4\sec on the curve. Let it strike at point X. So slope at this point is calculated by drawing a tangent at this point X, let the tangent line be AB.

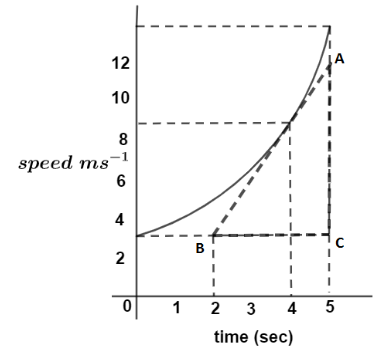
So slope of AB is defined as the value of tangent angle. So tangent angle is defined as, tan⁡θ=ACCB\tan \theta = \dfrac{{AC}}{{CB}}
Here, AC=(12−3)msec⁡−1AC = (12 - 3)m{\sec ^{ - 1}} and CB=(5−2)sec⁡CB = (5 - 2)\sec
Putting values we get,
tan⁡θ=(12−3)msec⁡−2(5−2)sec⁡\tan \theta = \dfrac{{(12 - 3)m{{\sec }^{ - 2}}}}{{(5 - 2)\sec }}
⇒tan⁡θ=9msec⁡−23sec⁡\Rightarrow \tan \theta = \dfrac{{9m{{\sec }^{ - 2}}}}{{3\sec }}
⇒tan⁡θ=3 m sec⁡−2\Rightarrow \tan \theta = 3\,m\,{\sec ^{ - 2}}
So slope is equal to, M=tan⁡θM = \tan \theta
M=3 m sec⁡−2M = 3\,m\,{\sec ^{ - 2}}
So, acceleration is 3 m sec⁡−23\,m\,{\sec ^{ - 2}}.

So the correct option is D.

Note: It should be remembered that acceleration can also be found if we know the velocity function of time, then the acceleration would be defined as a derivative of velocity function with respect to time. Also if the acceleration through motion is uniform in nature then we can use three equations of motions to calculate the locus and other constants like time, final velocity etc.