Question
Question: The curve \(y = \dfrac{{{x^2}}}{2}\) and the line \(y = \dfrac{x}{2}\) intersect at the origin and a...
The curve y=2x2 and the line y=2x intersect at the origin and at the point(a,b); as shown in the figure. Find the value of b.
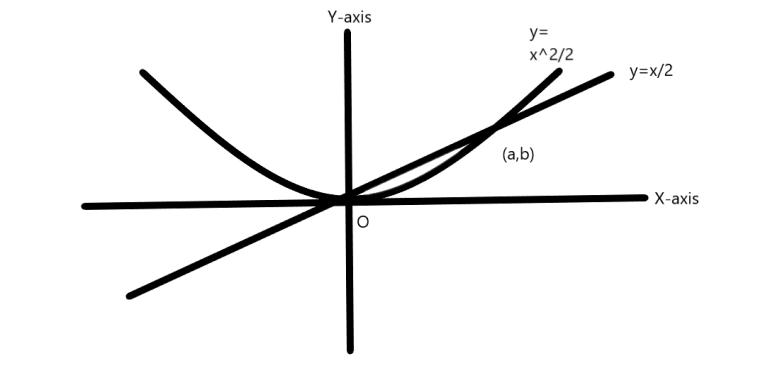
A. 81
B. 41
C. 21
D. 1
E. 2
Solution
We will assume an arbitrary point on the Cartesian plane and make it lie on the equation of both of the curves. We will solve the two equations in order to find the point of intersection. Then y-coordinate of the point of intersection will be equal to b.
Complete step by step answer:
Given
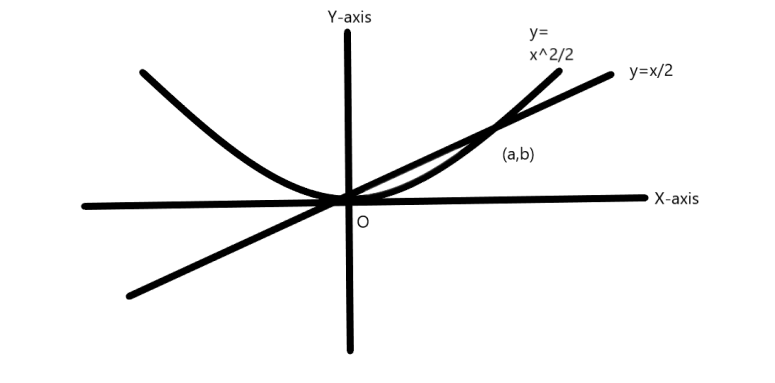
For two curves, there exists a point of intersection when the graphs of both curves intersect. It is obvious that the point of intersection lies on both curves and will satisfy the equations of both curves.
We have the following two curves:
y=2x2
y=2x
To find the intersection point of the above two curves, as given the point of intersection is (a,b), the point of intersection will lie on both the curves as per the definition of intersection point.
Thus, substituting (a,b)in first curve, we have
b=2a2 …(i)
Now, substituting (a,b)in second curve, we have
b=2a …(ii)
Substituting (i) in (ii)
⇒2a2=2a
⇒a2=a
⇒a2−a=0
⇒a(a−1)=0
Thus a=0 or a=1
For a=0, we have
b=2a
⇒b=20=0
For a=0it is the origin as point of intersection.
Now, fora=1, we have:
b=2a=21
Thus, another point of intersection of the curves is (1,21)
Comparing the above point of intersection with the given point (a,b)
We have b=21
Hence, option C is correct.
Note: Students must take care while calculating the point of intersection, it must be remembered that only point of intersection lies on given curves. Also, while calculating the point of intersection, students must not ignore any point, as each value of a variable corresponds to a specific point.
