Question

The curve represented parametrically by the equations $x=2\ln\cot t + 1$ and $y = \tan t + \cot t$

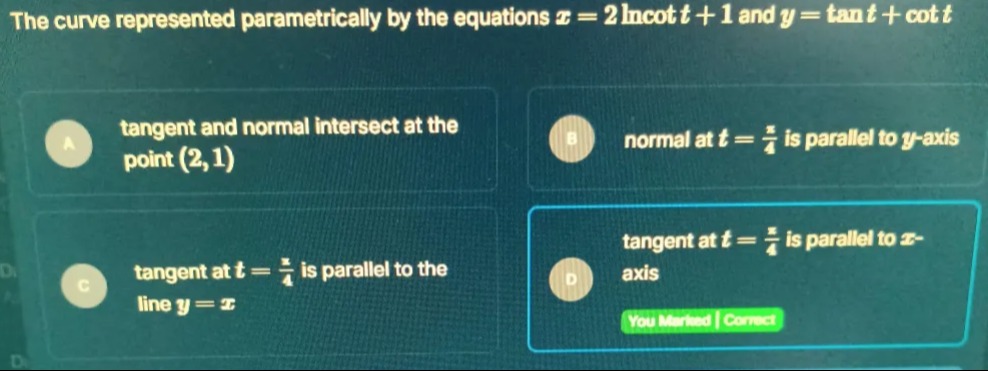
• A. tangent and normal intersect at the point (2, 1)
• B. normal at $t = \frac{\pi}{4}$ is parallel to $y$-axis
• C. tangent at $t = \frac{\pi}{4}$ is parallel to the line $y = x$
• D. tangent at $t = \frac{\pi}{4}$ is parallel to $x$-axis

Answer 1

Answer: (B), (D)

B and D

Answer 2

The derivatives are:

$\frac{dx}{dt}=-\frac{2}{\sin t\cos t}$

$\frac{dy}{dt}=\sec^2t - \csc^2t$

Thus,

$\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}} =\frac{\sec^2t-\csc^2t}{-\frac{2}{\sin t\cos t}} =-\frac{\sin t\cos t}{2}(\sec^2t-\csc^2t) =-\frac{1}{2}\left(\tan t-\cot t\right)$.

At $t=\frac{\pi}{4}$, slope is 0 so the tangent is horizontal (parallel to the $x$-axis) and the normal (perpendicular to the tangent) is vertical (parallel to the $y$-axis). The point on the curve at $t=\frac{\pi}{4}$ is $(1,2)$, not $(2,1)$.