Question

The curve for which the normal at any point $\left( {x,y} \right)$ and the line joining the origin to the points from the isosceles triangle with $x$–axis as a base, is
A. An ellipse
B. A rectangular hyperbola
C. A circle
D. None of the above

Answer 1

First we will first take the OPG is an isosceles triangle, ${\text{OM = MG = subnormal}}$. Taking the equation $x = y\dfrac{{dy}}{{dx}}$ by separating variables and then integrate it to find the equation for the final answer.

Complete step by step answer:

We are given that the curve for which the normal at any point $\left( {x,y} \right)$ and the line joining the origin to the points from the isosceles triangle with $x$–axis as a base.

It is given that the OPG is an isosceles triangle.

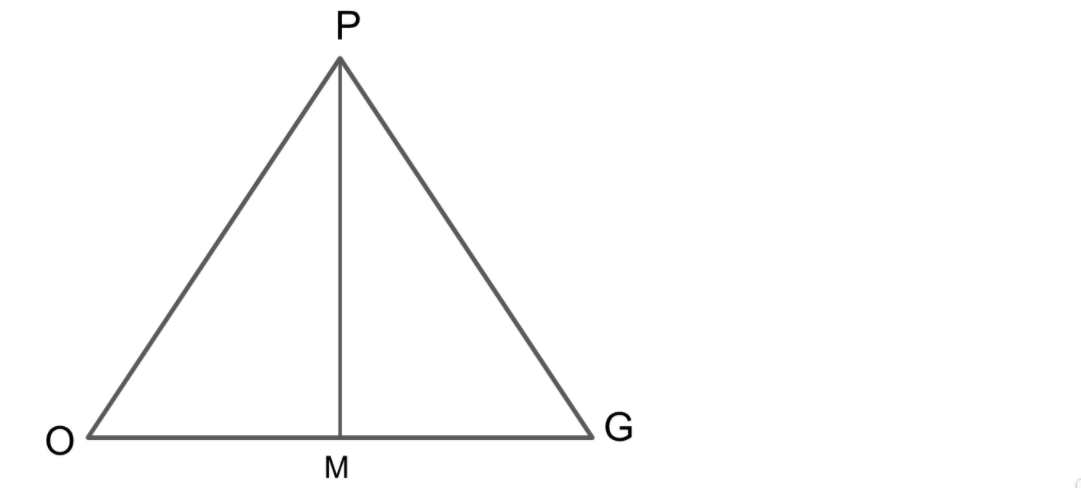
Therefore ${\text{OM = MG = subnormal}}$.

$$\Rightarrow x = y\dfrac{{dy}}{{dx}} \\\ \Rightarrow xdx = ydy \\\$$

Integrating the above equation on both sides, we get
$\Rightarrow \dfrac{{{x^2}}}{2} = \dfrac{{{y^2}}}{2} + c$
Multiplying the above equation by 3 on both sides, we get

$$\Rightarrow {x^2} = {y^2} + 2c \\\ \Rightarrow {x^2} - {y^2} = 2c \\\$$

Taking $a = 2c$ in the above equation, we get
$\Rightarrow {x^2} - {y^2} = a$
We know that the standard equation of the rectangular hyperbola ${\left( {x - {x_0}} \right)^2} + {\left( {y - {y_0}} \right)^2} = {a^2}$, where $\left( {{x_0},{y_0}} \right)$ is the point of intersection of hyperbola and $a$ is the length.
Compare the above equation with the standard equation of a rectangular hyperbola.
This implies that it is a rectangular hyperbola.
Hence, option B is correct.

Note: In solving these types of questions, the key concept is to know that when a triangle is an isosceles triangle, then the midlines are subnormal. Then we can easily find the equation of the curve to find the final answer.