Question

The current-voltage graph for a device is shown in figure. The resistance is negative in region:

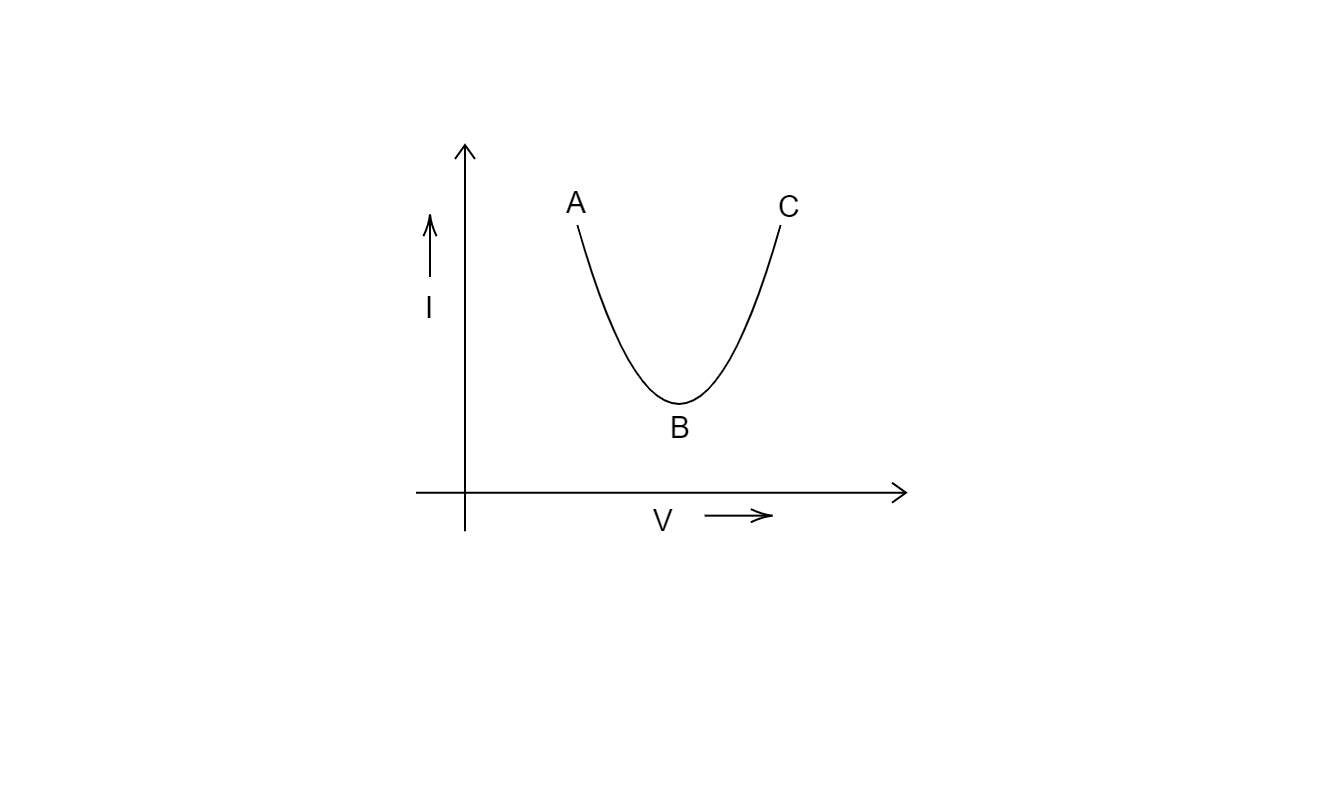
(a) AB
(b) BC
(c) ABC
(d) None of these

Answer 1

Resistance is given as $R = \dfrac{V}{I}$. Here the slope gives us the value $m = \dfrac{{\Delta I}}{{\Delta V}} = \dfrac{{{I_2} - {I_1}}}{{{V_2} - {V_1}}}$which is nothing but $m = \dfrac{1}{R}$. Therefore, try to figure for which part the slope will be negative.

Complete step by step answer:
From Ohm’s Law we have,
$V = IR \\\ \Rightarrow R = \dfrac{V}{I} \\\$
And the graph is I vs V so the slope will be,
$m = \dfrac{{\Delta I}}{{\Delta V}} = \dfrac{{{I_2} - {I_1}}}{{{V_2} - {V_1}}}$
On further simplification,
$R = \dfrac{1}{m}$
Now from the graph we see that for part AB the slope is negative, for point B slope is zero and for part BC the slope is positive. Therefore, the part for which the resistance is negative is AB.
The correct answer is option A.

Note: Be careful in evaluating the slope. Read the axes carefully whether V is on x-axis or y-axis. Many times students evaluate slope m=R=V/I in a hurry. Well the answer remains the same and correct in case of multiple choice. But in case of subjective questions, marks will be deducted.