Question

The current through the $1\,\Omega$ resistance is:

A. $2\,{\text{A}}$
B. $1\,{\text{A}}$
C. $3\,{\text{A}}$
D. None

Answer 1

In reversed biased condition, a diode does not allow current to flow through it. We also know that, if the same amount of current flows through a number of elements, then the elements are in series. We will use Ohm’s law to find the current.

Formula used:
We have Ohm’s law:
$V = iR$ …… (1)
Where,
$V$ indicates voltage.
$i$ indicates current flowing.
$R$ indicates resistance.

Complete step by step answer:
In the given question, we are supplied with the following data:
In the electric circuit, there are two diodes connected, where one is forward biased and the other is reversed biased.The voltage connected in the circuit is $6\,{\text{V}}$ .The three resistors are $1\,\Omega$ , $2\,\Omega$ and $2\,\Omega$ .We are asked to find the current flowing the $1\,\Omega$ resistor.

Let us proceed to solve the numerical.
First, we will redraw the circuit, by assigning names to the nodes and to identify the branches.

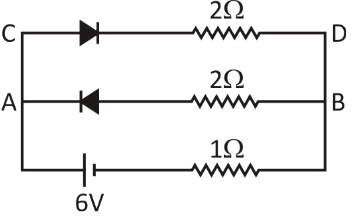
In the branch AB, as we can see that the diode is reversed biased, so there will be no flow of current in the branch AB. However, in the branch CD, there will definitely be current flow, as the diode is forward biased. So, it is clear that the AB can be removed as there will be no current flow. We again, now redraw the circuit for better understanding. The figure is given below:

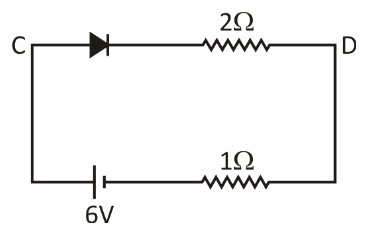
From the above circuit, it can be seen that the two resistors are in series.
From equation (1), we can find the current:
$V = iR \\\ \Rightarrow 6 = i \times \left( {2 + 1} \right) \\\ \Rightarrow 6 = i \times 3 \\\ \therefore i = 2\,{\text{A}}$
Hence, the current flowing through the $1\,\Omega$ resistance is $2\,{\text{A}}$ .

The correct option is A.

Note: While solving the problem, we must remember that most of the students do not consider the connection of the diodes. When the positive part of the diode is connected to the positive terminal of the battery, then it is called forward biased, in which the current flows. However, the positive part of the diode is connected to the negative terminal of the battery, then it is called reversed biased, in which the current does not flow and the resistance offered by the diode is very high. However, if the voltage is of very high order, then current will flow by causing a breakdown in the diode.