Question

The current in the adjoining circuit will be

A. $\dfrac{1}{45}ampere$
B. $\dfrac{1}{15}ampere$
C. $\dfrac{1}{10}ampere$
D. $\dfrac{1}{5}ampere$

Answer 1

When two resistances of are connected in series, their effective resistance is equal to the sum of the individual resistances. When two resistances are in parallel connection, the reciprocal of their effective resistance is equal to the sum of the reciprocals of the individual resistances.

Formula used:
${{R}_{eff}}={{R}_{1}}+{{R}_{2}}$
$\dfrac{1}{{{\operatorname{R}}_{eff}}}=\dfrac{1}{{{\operatorname{R}}_{1}}}+\dfrac{1}{{{\operatorname{R}}_{2}}}$
where ${{R}_{1}}$ and ${{R}_{2}}$ are the two resistances.
$V=iR$
Where, V is the emf of the cell, i is the current in the circuit and R is the net resistance of the circuit.

Complete step by step answer:
The above given circuit contains a combination of three resistances. It is little difficult to find the current flowing through the cell by analysing the three resistances separately. Therefore, we shall find the effective resistance of the three resistances and replace all three by one resistance. Then we just need one formula for calculating the current.

We can see the outer three resistances are connected in series. When two resistances of are connected in series, their effective resistance is equal to the sum of the individual resistances. i.e. ${{R}_{eff}}={{R}_{1}}+{{R}_{2}}$, where ${{R}_{1}}$ and ${{R}_{2}}$ are the two resistances.

In this case, ${{R}_{1}}={{R}_{2}}=30\Omega$.
And let the effective resistance of these resistances be ${{R}_{eff,1}}$.
Therefore, ${{R}_{eff,1}}=30+30=60\Omega$.
Now, the given circuit can be redrawn as:

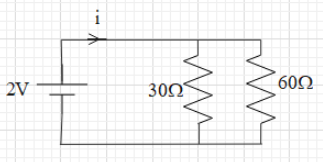
Now, we can see that the two resistances are in parallel connection. When two resistances are in parallel connection, the reciprocal of their effective resistance is equal to the sum of the reciprocals of the individual resistances.
i.e. $\dfrac{1}{{{\operatorname{R}}_{eff}}}=\dfrac{1}{{{\operatorname{R}}_{1}}}+\dfrac{1}{{{\operatorname{R}}_{2}}}$.
In this case, $\dfrac{1}{{{\operatorname{R}}_{eff}}}=\dfrac{1}{30}+\dfrac{1}{60}=\dfrac{3}{60}=\dfrac{1}{20}$
$\Rightarrow {{\operatorname{R}}_{eff}}=20\Omega$.
Therefore, the effective resistances of the above circuit is $20\Omega$.

So now we can think that instead of the given combination of resistances, the circuit has a single resistance of $20\Omega$. From Ohm’s law we know that $V=iR$, V is the emf of the cell, i is the current in the circuit and R is the net resistance of the circuit. In this case,
$V=2volts$ and $R=20\Omega$.
$2=i(20)$
$\Rightarrow i=\dfrac{2}{20}\\\ \therefore i=\dfrac{1}{10}ampere$.
Therefore, the current in the circuit is $\dfrac{1}{10}ampere$.

Hence, the correct option is C.

Note: Note that the above formulae are applicable for more than two resistances also. If there are ‘n’ resistances connected in series, then their effective resistance is given as ${{R}_{eff}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+.......+{{R}_{n}}$.
If there are ‘n’ resistances connected in parallel, then the effective resistance of this combination is written as, $\dfrac{1}{{{R}_{eff}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}+.......+\dfrac{1}{{{R}_{n}}}$.