Question
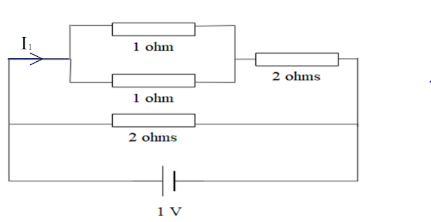
Question: The current I1 (in A) flowing through the 1 Ω resistor in the below circuit is,  flowing through the 1 Ω resistor in the below circuit is,
(A) 0.25
(B) 0.2
(C) 0.5
(D) 0.4
Solution
Hint
To find out the current flowing through the given resistor, first we need to know about the laws defining the given figure. We need to study ohm's law, which states that the potential difference between two points is directly proportional to the current flowing through the circuit. First, we need to find the total resistance in the top branch, then we need to apply the law to find out the current flowing through it.
Formula used:
Itotal=RtotalV where V is the potential difference, Itotal is the current in the circuit and Rtotal is the net resistance.
Complete step by step answer
Let us understand the given quantities in the circuit,
The potential difference in the top most branch is V=1V,
R1 and R2 are 1 ohms each,
Now, we need to calculate the total resistance of the branch.
Using the formula for the effective resistance in series,
Rtotal=Rp+2Ω ….. eq. 1
By using the formula for resistance in parallel,
Rp=(R1+R2R1×R2)
By substituting the values of R1 and R2 ,
Rp=(1+11×1)
⇒Rp=0.5Ω
Now substitute the value in eq. 1,
\begin{array}{*{20}{l}}
{{R_{total}} = 0.5{\text{ + }}2} \\\
{ \Rightarrow {R_{total}} = 2.5\Omega }
\end{array}
Now, according to ohm’s law,
Itotal=RtotalV
⇒Itotal=2.51
Thus, we get,
⇒Itotal=0.4A
Now, we know that the potential differences in the two branches are the same and the current divides into I1 and I2.
⇒V=I1R1=I2R2
And the total I = I1 + I2. Then,
\begin{array}{*{20}{l}}
{{I_1}{R_1} = {I_2}{R_2}} \\\
{ \Rightarrow {I_1}{R_1} = \left( {{\text{ }}I{\text{ }} - {\text{ }}{I_1}} \right){\text{ }}{R_2}}
\end{array}
Thus,
⇒I1( R1+ R2)=I2R2
To find I1,
I1= ( R1+ R2)I2R2
By substituting the values of the quantities,
I1=1+10.4×1
⇒I1=0.2A
Thus, the correct answer is option B.
Note
While calculating the current flowing through the branches, keep in mind that the potential difference across the branches is the same in this type of circuit and the current is divided in the junction.
