Question

The current I through the cell in the network shown in

(A) 3A
(B) 2A
(C) 1A
(D) 4A

Answer 1

Hint We know that the equivalent resistance is where the aggregate resistance connected either in parallel or series is calculated. Electrical resistance shows how much energy one needs when we move the charges or current through the devices. The method we use to calculate equivalent resistance is different for each type of circuit. For a series circuit, we simply add up the resistances of each component. However, in a parallel circuit, the reciprocal of the total resistance is equal to the sums of the reciprocals of the resistances of each branch. Based on this we have to solve this question.

Complete step by step answer
Let us begin the answer by drawing the resistive diagrams for the series and parallel connections in the above diagram separately.
Now, at first let us draw the series diagram for the above connection at first:

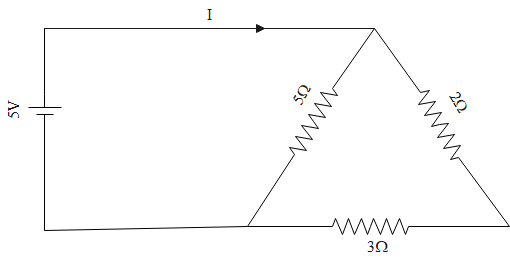
The resistances 2 and 3 are in the series connection. So, the final resistance is given as:
$R=(2+3)\Omega =5\Omega$
Now, we have to draw the parallel diagram for the above connection:

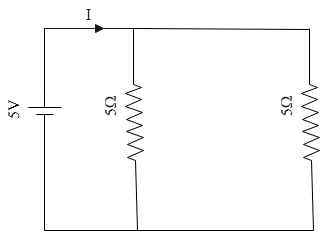
In the above diagram we can see that the resistances, 5 and 5 are in parallel connection.
Hence the required total resistance is given as:
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{5}+\dfrac{1}{5}=\dfrac{2}{5}$
Thus, we can say that
${{R}_{eq}}=\dfrac{5}{2}=2.5\Omega$ ${{R}_{eq}}=\dfrac{5}{2}=2.5\Omega$
Now, we have to draw the diagram for the voltage, which is given below:

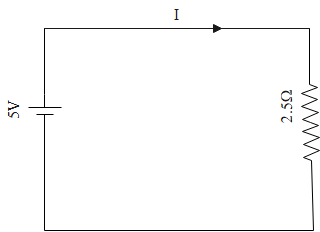
From the diagram we can say that the formula for voltage is given as:
$V=IR$
$\Rightarrow I=\dfrac{V}{R}$
Now we have to put the values to get:
$I=\dfrac{5}{2.5}=2A$

Hence, the correct answer is option B.

Note Thus, we can conclude that in a series circuit, the output current of the first resistor flows into the input of the second resistor; therefore, the current is the same in each resistor. In a parallel circuit, all of the resistor leads on one side of the resistors are connected together and all the leads on the other side are connected together. The equivalent resistance of a series circuit compared to the resistance values of the individual resistances in the circuit has a higher value. The equivalent resistance of a series circuit is calculated as the sum of all the individual resistances which gives it a larger value than the individual. The amount of current in a series circuit is the same through any component in the circuit. This is because there is only one path for current flow in a series circuit. If the two resistances or impedances in parallel are equal and of the same value, then the total or equivalent resistance, is equal to half the value of one resistor.