Question
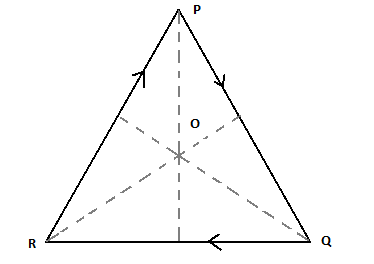
Question: The current \(I\) is flowing in an equilateral triangle of side \(a\) as shown in figure. The magnet...
The current I is flowing in an equilateral triangle of side a as shown in figure. The magnetic field at the centroid O will be:
A) 2πa9μ0I
B) 3πa52μ0I
C) 2πa3μ0I
D) 33πaμ0I
Solution
Use the Biot-savart’s law to calculate the magnetic field on one side of the triangle,
B=4πμ0×rI×(sinθ+sinθ)
B is magnetic field intensity,
I is the current intensity,
μ0 is the permeability of free space.
Complete step by step solution:
The Biot – Savart Law is an equation that defines a steady electric current produced by the magnetic field. It refers to magnitude, direction, length and proximity of the electrical current in the magnetic field. The Biot-Savart’s law is important for magneto-statics, and plays a similar role in the electrostatics law of Coulomb. If magneto statics are not applicable, Jefimenko equations can replace the Biot-Savart’s rule. The rule shall be in line with both the circuit rules of Ampere and the magnet law of Gauss. Let’s consider that an angle θ is made by each end of each side at centroid is600 and r is the perpendicular distance of each side from centroid which is equal to63a.
Using Biot-savart's law, magnetic field at the centroid by each side can be written as,
B=4πμ0×rI×(sinθ+sinθ)
B is magnetic field intensity,
I is the current intensity,
μ0 is the permeability of free space.
Putting all the values given in the question, we get,
B=4πμ0×3a6I×(sin60+sin60)
⇒B=4πμ0×3a6I×3
⇒B=4πμ0×a6I
Total magnetic field on all the three sides of the equilateral triangle will be three times the calculated magnetic field,
B′=3B
⇒B′=4πμ0×a6I×3
⇒B′=4πμ0×a9I
The magnetic field at the centroid O will be 2πa9μ0I.
Hence, the correct option is A.
Note: In a plane perpendicular to the element line and the location vector always the direction of the magnetic field. The left thumb rule is given where the thumb points towards the current position and the other fingers shows the direction of the magnetic field.
