Question
Question: The current I in the circuit shown is _______....
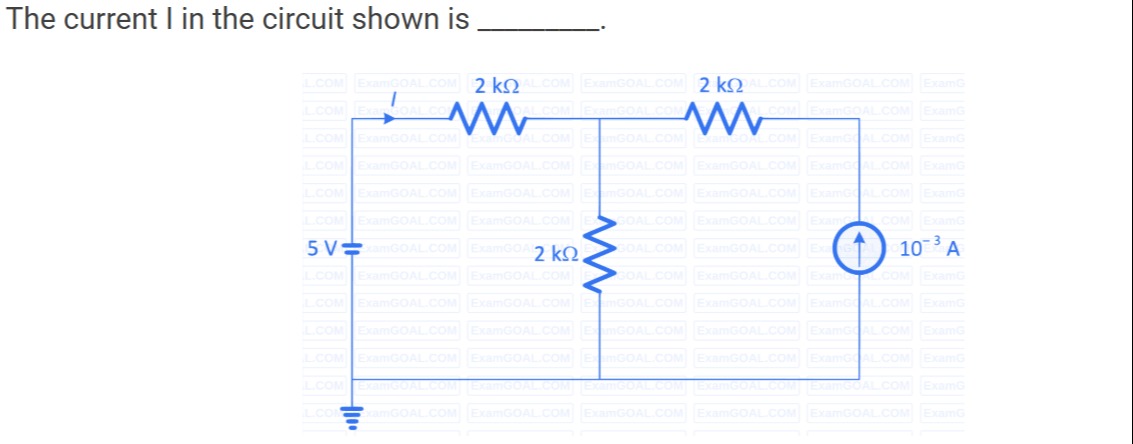
The current I in the circuit shown is _______.
3.25 x 10^{-3} A
Solution
The problem asks us to find the current 'I' in the given circuit. We can solve this using nodal analysis or the superposition theorem. Nodal analysis is generally more straightforward for circuits with multiple sources and interconnected nodes.
1. Define Nodes and Voltages: Let the bottom wire be the ground reference (0 V). Let the node connected to the positive terminal of the 5V voltage source be Node 1. From the diagram, the 5V source is connected between Node 1 and ground, so the potential at Node 1 is V1=5 V. The current 'I' is the total current flowing out of the 5V source into Node 1. Let the node between the two horizontal 2 kΩ resistors and the vertical 2 kΩ resistor be Node 2, with potential V2. Let the node between the rightmost horizontal 2 kΩ resistor and the current source be Node 3, with potential V3.
2. Apply Kirchhoff's Current Law (KCL) at Node 2 and Node 3:
KCL at Node 2 (V2): The sum of currents leaving Node 2 must be zero. Current from Node 1 to Node 2: 2 kΩV2−V1 Current from Node 2 to Node 3: 2 kΩV2−V3 Current from Node 2 to Ground: 2 kΩV2−0
So, we have: 2 kΩV2−V1+2 kΩV2−V3+2 kΩV2=0 Multiply by 2 kΩ: (V2−V1)+(V2−V3)+V2=0 Substitute V1=5 V: (V2−5)+(V2−V3)+V2=0 3V2−V3−5=0 3V2−V3=5(Equation 1)
KCL at Node 3 (V3): The sum of currents leaving Node 3 must be zero. Current from Node 2 to Node 3: 2 kΩV3−V2 Current from the current source: The arrow indicates current flowing from ground to Node 3, so it's an incoming current of 10−3 A. If we consider currents leaving the node as positive, then the current due to the source leaving Node 3 is −10−3 A.
So, we have: 2 kΩV3−V2−10−3=0 2000V3−V2=10−3 V3−V2=2000×10−3 V3−V2=2(Equation 2)
3. Solve the System of Equations: We have two linear equations with two unknowns (V2 and V3):
- 3V2−V3=5
- −V2+V3=2
Add Equation 1 and Equation 2: (3V2−V3)+(−V2+V3)=5+2 2V2=7 V2=27=3.5 V
Substitute V2=3.5 V into Equation 2: V3−3.5=2 V3=2+3.5 V3=5.5 V
4. Calculate the Current 'I': The current 'I' is the total current leaving the 5V source and entering Node 1. This current splits into two branches:
- Current flowing from Node 1 to Node 2 through the 2 kΩ resistor: I12=2 kΩV1−V2
- Current flowing from Node 1 to Ground through the 2 kΩ resistor: I1G=2 kΩV1−0
Therefore, I=I12+I1G I=2000V1−V2+2000V1 Substitute V1=5 V and V2=3.5 V: I=20005−3.5+20005 I=20001.5+20005 I=20001.5+5 I=20006.5 I=2×1036.5 I=3.25×10−3 A Or, I=3.25 mA.
