Question

The current$\;I$ and voltage$\;V$ graphs for a given metallic wire at two different temperatures $T_1$ and $T_2$ are shown in the figure. It is concluded that:

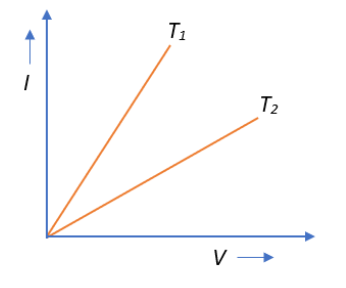
A. $T_1 > T_2$
B. $T_1 < T_2$
C. $T_1=T_2$
D. $T_1 = 2T_2$

Answer 1

We know that the slope of a V-I graph gives the resistance of an Ohmic element. In such a case, given the above graph, determine the relation between the resistance of the Ohmic element at the two temperatures. To this end, using the dependency of resistance on temperature and its variation, arrive at the appropriate relation for the temperature. Remember that the thermal energy supplied gets absorbed by the ions in a conductor, which then vibrate about their mean positions.

Formula used: Ohm’s Law: $V = RI$

Complete step by step answer:
We know Ohm’s Law states that the voltage across a conductor is directly proportional to the current flowing through it:
$V\propto I \Rightarrow V=RI \Rightarrow R = \dfrac{V}{I}$, where R is the resistance offered by the conductor.
Therefore, if we plotted the voltage across the y-axis and the current across the x-axis for an Ohmic element, the slope of the V-I graph would yield the resistance of the element because like we discussed above,
$tan\;\theta = R = \dfrac{V}{I}$, where $\theta$ is the angle through which the slope is inclined from the x-axis.
However, we are given an I-V graph, so the slope of the I-V graph will yield:
$tan\;\theta = \dfrac{I}{V} = \dfrac{1}{R}$, which is the reciprocal of resistance.
Thus, from the given graph, we see that:
$\theta_1 > \theta_2$
$\Rightarrow \dfrac{1}{R_1} > \dfrac{1}{R_2}$
$\Rightarrow R_2 > R_1$
Now, let us look at the resistance and temperature relationship for any conductor. We know that as the temperature increases, the rate at which the fixed ions in a conductor absorb the heat and thermally vibrate about their mean positions increases, which drastically increments their likelihood of colliding with electrons that are drifting across, thereby impeding their motion as they pass through. This means that the resistance to the flow of electrons increases with increasing temperature, i.e.,
$R\propto T$
This implies that since
$R_2 > R_1 \Rightarrow T_2 > T_1$

So, the correct answer is “Option B”.

Note: Do not get confused between resistance and resistivity.
Resistance is a measure of the opposition that an object offers to a flow of current, whereas resistivity is a characteristic property of the material making up the object which resists the flow of current through it.
Resistance of a wire is dependent on the length, cross-sectional area and temperature of the wire, whereas its resistivity is dependent only on the material and temperature of the wire. Thus, the resistivity of a wire remains the same with a change in the length or area of the wire but changes with variations in temperature.
The two are related as: $R=\rho \dfrac{l}{A}$, where R is the resistance, $\rho$ is the resistivity, l is the length of the conductor and A is its area of cross-section.