Question

The cross sectional area of a horizontal tube increases along its length linearly, as we move in the direction of flow. The variation of pressure, as we move along its length in the direction of flow (x-direction), is best depicted by which of the following graphs.
(A).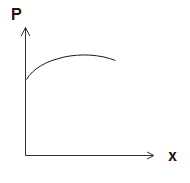
(B).
(C).
(D).

Answer 1

Area increases with distance along the x-axis as it is directly proportional to x. According to the continuity equation, the product of area and velocity always remains constant in a one-directional flow. Bernoulli's equation gives a relation between pressure and velocity. Using these relations we can find the required relation between pressure and distance along the x-axis.

Formulas Used:
$Av=\text{constant}$
$P+\dfrac{\rho {{v}^{2}}}{2}=c'$

Complete answer:
When a fluid is in motion, it moves so that the mass is always conserved. According to the law of continuity, for a flowing liquid,
$Av=\text{constant}$
$v=\dfrac{c}{A}$ ---- (1)
Here, $A$ is the area of the cross-section from which the fluid passes through
$v$is the velocity
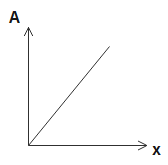
Given, that area of the cross-section of a tube increases linearly, so the graph between $x$and area is a straight line.
$A\propto x$
$A=kx$ ---- (2)

Bernoulli’s equation gives a relationship between pressure and velocity, for a horizontal tube it is given as-
$P+\dfrac{\rho {{v}^{2}}}{2}=c'$ ---- (3)
Here, $P$ is the pressure
$\rho$ is the density of the fluid
From eq (1), eq (2), and eq (3), we have,
$P+\dfrac{\rho }{2{{k}^{2}}{{x}^{2}}}=c'$
The above equation is the equation of a parabola with concave downwards. Therefore, the relation between $P\, and\,x$ depicts a parabola facing downwards.

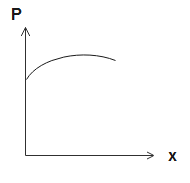
So, the correct option is (A).

Note:
The equation of continuity is given for the one-dimensional flow of liquid with only one inlet and one outlet. Bernoulli’s principle says that when the velocity of fluid increases, its potential energy decreases. Bernoulli's principle follows the law of conservation of energy, i.e. sum of all energies possessed by the flowing fluid is constant.