Question

The cross-sectional area and the length of a cylindrical conductor are $A$ and $l$ respectively. The specific conductivity varies as $\sigma \left( x \right) = {\sigma _0}l\sqrt x$ where $x$ is the distance along the axis of the cylinder from one of its ends.

i) Compute the resistance of the system along the cylindrical axis.
ii) Find the electric field at each point in the cylinder in the above case.

Answer 1

The resistance of the given conductor depends on the resistivity, length and area of the conductor. To compute the resistance of the system we should first consider a small elemental cross sectional area of the given conductor and obtain an expression for its resistance. Integrating this expression for the length of the cylinder will provide us with the resistance of the system. We can then use Ohm’s law to find the current and current density of the conductor to determine the electric field at each point of the conductor.

Formulae used:
The resistance of a conductor is given by, $R = \dfrac{l}{{\sigma A}}$ where $l$ is the length of the conductor, $A$ is its cross sectional area and $\sigma$ is its conductivity.
Ohm’s law gives the current through some conductor as $I = \dfrac{V}{R}$ where $V$ is the potential difference across the conductor and $R$ is the resistance of the conductor.
The current density of a conductor is given by, $J = \dfrac{I}{A}$ where $I$ is the current through the conductor and $A$ is the cross sectional area of the conductor.
The electric field at a point along a conductor is given by, $E = \dfrac{J}{\sigma }$ where $J$ is the current density and $\sigma$ is the conductivity of the conductor.

Complete step by step answer:
Step 1: Sketch the conductor and consider a small elemental area of it.
In the above figure, we consider a small elemental area of resistance ${\text{dR}}$ at a distance $x$ from one of the ends of the cylindrical conductor and width ${\te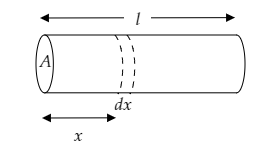xt{dx}}$ .
The length of the conductor is given to be $l$ and its area of cross-section is given to be $A$ .
Also, the specific conductivity is expressed as a function of the distance $x$ from its end as $\sigma \left( x \right) = {\sigma _0}l\sqrt x$ .
Now the resistance of the small elemental area can be expressed as
$dR = \dfrac{{dx}}{{\sigma A}} = \dfrac{{dx}}{{{\sigma _0}l\sqrt x A}}$ -------- (1)
Step 2: Integrate equation (1) to obtain the resistance of the system.
Integrating equation (1) for the length of the conductor we get the resistance of the entire conductor as $R = \int\limits_0^l {dR} = \int\limits_0^l {\dfrac{{dx}}{{{\sigma _0}l\sqrt x A}}}$
Simplifying the integral we get, $R = \dfrac{1}{{{\sigma _0}lA}}\int\limits_0^l {\dfrac{{dx}}{{\sqrt x }}} = \dfrac{1}{{{\sigma _0}lA}}\left[ {2\sqrt x } \right]_0^l$ ----------- (A)
Applying the limits we obtain $R = \dfrac{{2\sqrt l }}{{{\sigma _0}lA}} = \dfrac{2}{{{\sigma _0}\sqrt l A}}$ .
$\therefore$ the resistance of the system is computed to be $R = \dfrac{2}{{{\sigma _0}\sqrt l A}}$ .
Step 3: Using Ohm’s law obtain the current and current density of the conductor.
Let the conductor be connected to a cell so that a potential difference $V$ exists across the conductor and a current $I$ flows through it.
According to Ohm’s law, the current through the conductor can be expressed as $I = \dfrac{V}{R}$ ------ (2)
Substituting for $R = \dfrac{2}{{{\sigma _0}\sqrt l A}}$ in equation (2) we get the current through the conductor as $I = \dfrac{{V{\sigma _0}\sqrt l A}}{2}$ -------- (3)
The current density will be expressed as $J = \dfrac{I}{A}$ -------- (4)
Substituting equation (3) in (4) we obtain the current density as
$J = \dfrac{{V{\sigma _0}\sqrt l A}}{{2A}} = \dfrac{{V{\sigma _0}\sqrt l }}{2}$
Thus the current density is obtained to be $J = \dfrac{{V{\sigma _0}\sqrt l }}{2}$ .
Step 4: Express the relation for the electric field along the conductor.
The electric field at a point along the axis of the conductor can be expressed as
$E\left( x \right) = \dfrac{J}{\sigma }$ ------- (5)
Substituting for $J = \dfrac{{V{\sigma _0}\sqrt l }}{2}$ and $\sigma \left( x \right) = {\sigma _0}l\sqrt x$ in equation (5) we get, $E\left( x \right) = \dfrac{{V{\sigma _0}\sqrt l }}{{2{\sigma _0}l\sqrt x }} = \dfrac{V}{{2\sqrt l }}\left( {\dfrac{1}{{\sqrt x }}} \right)$
$\therefore$ the electric field at any point in the conductor is obtained to be $E\left( x \right) = \dfrac{V}{{2\sqrt l }}\left( {\dfrac{1}{{\sqrt x }}} \right)$.

Note: It is always easier to integrate a function if all the constants involved are taken outside the integral before integrating the function. Equation (A) was integrated using the relation $\int {{x^n}dx} = \dfrac{{{x^{n + 1}}}}{{n + 1}}$ and in equation (A), $n = \dfrac{{ - 1}}{2}$ as $\dfrac{1}{{\sqrt x }} = {x^{ - 1/2}}$. Current density refers to the amount of current flowing through a given area. The specific conductivity is essentially the reciprocal of resistivity so we express the resistance of the small elemental area as that given by equation (1).