Question

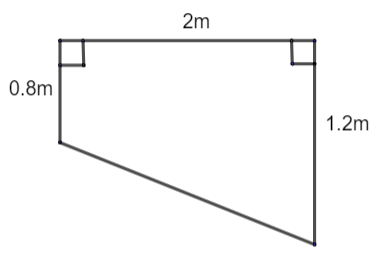
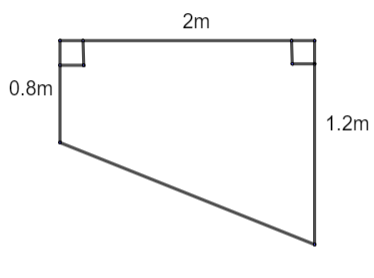
The cross – section of a swimming pool is a trapezium as shown in the adjacent diagram. The length of the pool is 200m. Water is pumped into it through a pipe of cross section $1.2{{m}^{2}}$ at a speed of 0.5 km/hr. Find the time needed to fill the pool completely.

Answer 1

Calculate the area of the trapezium pool by using the formula: - Area = $\dfrac{1}{2}\times$ (sum of parallel lines) $\times$ distance between the parallel lines. Now, find the volume of the pool by taking the product of Area and the given length of pool. Now, find the volume of water flowing through the pipe by considering the product of cross – section of pipe and speed of water. Multiply the given speed with 1000 to convert it into m/hr. Finally, apply the formula: - Time = (Volume of pool / Volume of water flowing), to determine the required time.

Complete step-by-step answer:
Here, we have been provided a pool with a given cross – section and length and we have to determine the time in which the pool will be filled with water with a given speed and area of cross – section.

Now, the above pool is in the shape of a trapezium, so we have,
$\Rightarrow$ Area of the pool = $\dfrac{1}{2}\times$ (sum of parallel lines) $\times$ distance between the parallel sides
$\Rightarrow$ Area of the pool = $\dfrac{1}{2}\times$ $\left( 0.8+1.2 \right)\times 2$
$\Rightarrow$ Area of the pool = $2{{m}^{2}}$
We know that volume is the product of the area of cross – section and length or height of the object. Here, the length of pool is 200m, so we have,
$\Rightarrow$ Volume of the pool = Area $\times$ length
$\Rightarrow$ Volume of the pool = 2 $\times$ 200
$\Rightarrow$ Volume of the pool = 400${{m}^{3}}$
Now, it is given that the pool is being filled with water with a pipe whose area of cross – section is $1.2{{m}^{2}}$ and speed of pumping the water is 0.5 km/hr. Converting the speed in m/hr, we get,

& \Rightarrow 0.5km/hr=0.5\times 1000m/hr\left( \because 1km=1000m \right) \\\ & \Rightarrow 0.5km/hr=500m/hr \\\ \end{aligned}$$ Here, we have to find the volume of water coming out of the pipe in one hour which will be the product of area of pipe and speed of water. So, we have, $$\Rightarrow $$ Volume of water coming out of the pipe in one hour = Area $$\times $$ speed $$\Rightarrow $$ Volume of water coming out of the pipe in one hour = 1.2 $$\times $$ 500 $$\Rightarrow $$ Volume of water coming out of the pipe in one hour = 600$${{m}^{3}}$$ Now, time taken by pipe to fill 600$${{m}^{3}}$$ = 1 hour $$\Rightarrow $$ Time taken by pipe to fill 1$${{m}^{3}}=\dfrac{1}{600}$$hour $$\Rightarrow $$ Time taken by pipe to fill 400$${{m}^{3}}=\dfrac{400}{600}$$hour = $$\dfrac{2}{3}$$hour Converting the obtained time into minutes, we get, $$\Rightarrow $$$$\dfrac{2}{3}$$hour = $$\dfrac{2}{3}\times 60$$min = 40 min ($$\because $$ 1hour = 60 min) Hence, the time taken by pipe to fill the pool is 40 minutes. **Note:** One must note that we have to convert the given speed of flowing water from km/hr to m/hr. This is because we have to find the volume in $${{m}^{3}}$$ unit. You must remember how to calculate the area of a trapezium and volume of different things from their given area and lengths to solve the question. Note that we have used the unitary method to find the time taken to fill the pool. You may use the direct formula given as: - Time = (Volume of pool / Volume of water flowing), to get the same answer.