Question

The couple acting on a bar magnet of pole strength 2 Am when kept in a magnetic field of intensity is 10 A/m, such that axis of the magnet makes an angle ${{30}^{\circ }}$ with the direction of the field is $80\times {{10}^{-7}}Nm$. The distance between the poles of the magnet is :
$\text{A}\text{. }8\times {{10}^{-9}}m$
$\text{B}\text{. }\dfrac{2}{\pi }m$
$\text{C}\text{. 63}\text{.36}m$
$\text{D}\text{. }\dfrac{1}{2\pi }m$

Answer 1

Find the magnet field in which the bar magnet is placed. For this use the relation between the magnetic field and the magnetic field intensity. Then use the formula for torque created by the magnetic force to find the distance between the poles.

Formula used:
$\tau =MB\sin \theta$
$B={{\mu }_{0}}H$

Complete step-by-step answer:
A bar magnetic is considered as a dipole. The dipole is made up of two poles separated by distance 2a. We define a quantity called pole strength of the poles (m and -m). The dipole moment of the magnetic dipole is given as M = 2am.
Consider a bar magnet placed in a uniform magnetic field of magnitude B. Suppose, the axis of the bar magnet is making an angle $\theta$ with the magnetic field vector.

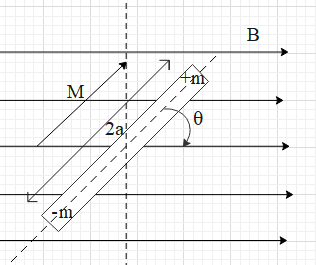
Then the magnetic force acting on the magnet creates a torque on the magnetic given as $\overrightarrow{\tau }=\overrightarrow{M}\times \overrightarrow{B}$.
Hence, the magnitude of the torque will be equal to $\tau =MB\sin \theta$ …… (i).
In the question, the values of $\theta$ , pole strength (m) and the torque ($\tau$) are given.
i.e. $\theta ={{30}^{\circ }}$, m = 2Am and $\tau =80\times {{10}^{-7}}Nm$.
The value of magnetic field (B) is not given. However, we can find its value with magnetic field intensity (H).
The relation between B and H is given as $B={{\mu }_{0}}H$.
It is given that $H=10A{{m}^{-1}}$. And the value of ${{\mu }_{0}}=4\pi \times {{10}^{-7}}Tm{{A}^{-1}}$ .
$\Rightarrow B={{\mu }_{0}}H=\left( 4\pi \times {{10}^{-7}} \right).\left( 10 \right)={{\mu }_{0}}=40\pi \times {{10}^{-7}}T$.
Substitute the known values in equation (i).
$\Rightarrow 80\times {{10}^{-7}}=\left( 2\times a\times 2 \right)\left( 40\pi \times {{10}^{-7}} \right)\sin 30$
$\Rightarrow 80\times {{10}^{-7}}=\left( 2\times a\times 2 \right)\left( 40\pi \times {{10}^{-7}} \right)\left( \dfrac{1}{2} \right)$
$\Rightarrow 2a=\dfrac{2}{\pi }m$.
This means that the distance between the poles of the magnet is equal to $\dfrac{2}{\pi }m$.

So, the correct answer is “Option B”.

Note: Actually, the distance between the poles of the magnetic is the length of the magnet. Therefore, the length of the given bar magnetic is $\dfrac{2}{\pi }m=0.66m$.
Students may make a mistake by taking the value of magnetic field intensity as the value of magnetic field B. We already discussed the relation between B and H.
Therefore, be careful while reading the question.
You can even make out the difference by the units of the two.
The unit of B is T and the unit of H is A/m.