Question

The cosine of the obtuse angle formed by medians drawn from the vertices of the acute angles of an isosceles right angled triangle is,
$({\text{A}})\,\dfrac{{ - 1}}{5} \\\ ({\text{B}})\,\dfrac{{ - 2}}{5} \\\ ({\text{C}})\,\dfrac{{ - 3}}{5} \\\ ({\text{D}})\,\dfrac{{ - 4}}{5} \\\$

Answer 1

The first step is to find the slope of the two medians. By using the angle between the two lines formula, we can find the tangent angle. In question they have asked the cosine of the obtuse angle, so we have to calculate accordingly by using tan theta.

Formula used
The Pythagoras theorem is used in this question which states that the square of the length of hypotenuse is equal to the sum of the square of the other two sides.
The slope of the line is,
${\text{m1 = }}\dfrac{{{\text{y2}} - {\text{y1}}}}{{{\text{x2}} - {\text{x1}}}}$
The angle between two lines of the triangle is,
${\text{tan}}\theta = \left| {\dfrac{{{\text{m1}} - {\text{m2}}}}{{{\text{1 + m1m2}}}}} \right|$
Where,
${\text{x1,x2}}$ be the axis of the ${\text{x}}$ formed by the line segment
${\text{y1,y2}}$ be the axis of the ${\text{y}}$ formed by the line segment
${\text{m1,m2}}$ be the gradient of the two lines

Complete step-by-step answer:
The data given in the question is,
The isosceles right-angled triangle $\vartriangle {\text{ABC}}$ is drawn below,
Let ${\text{a}}$ be the length of the two sides of the isosceles right-angled triangle

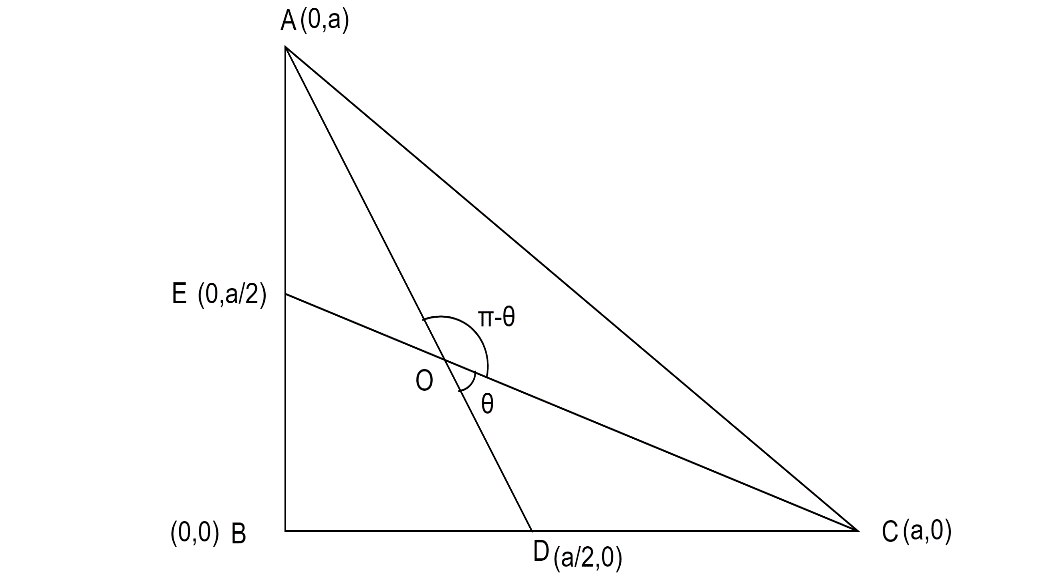
${\text{AD}}$ and ${\text{CE}}$ are the medians drawn from the vertices which intersect at the point ${\text{O}}$
$\theta$ be the angle made by the medians which forms the triangle $\vartriangle {\text{DOC}}$
$\pi - \theta$ be the angle made by the medians which forms the triangle $\vartriangle {\text{AOC}}$

To find the cosine of the obtuse angle,

Step 1
The slope of the median ${\text{CE}}$ in the above triangle be ,
${\text{m1 = }}\dfrac{{{\text{y2}} - {\text{y1}}}}{{{\text{x2}} - {\text{x1}}}}$
While substituting the values of ${\text{x and y}}$ axes in the above we get,
${\text{m1 = }}\dfrac{{\dfrac{{\text{a}}}{2} - 0}}{{0 - {\text{a}}}}$
While solving we get the slope of the median ${\text{CE}}$,
${\text{m1 = }}\dfrac{{ - 1}}{2}$
The slope of the median ${\text{AD}}$ in the above triangle be ,
${\text{m2 = }}\dfrac{{{\text{y2}} - {\text{y1}}}}{{{\text{x2}} - {\text{x1}}}}$
While substituting the values of ${\text{x and y}}$ axes in the above we get,
${\text{m2 = }}\dfrac{{0 - {\text{a}}}}{{\dfrac{{\text{a}}}{2} - 0}}$
While solving we get the slope of the median ${\text{AD}}$,
${\text{m2 = }} - 2$

Step 2
The angle between the two lines of the triangle is,
${\text{tan}}\theta = \left| {\dfrac{{{\text{m1}} - {\text{m2}}}}{{{\text{1 + m1m2}}}}} \right|$
While substituting the gradient values in the above we get,
${\text{tan}}\theta = \left| {\dfrac{{\dfrac{{ - 1}}{2} - ( - {\text{2)}}}}{{{\text{1 + (}}\dfrac{{ - 1}}{2}{\text{)(}} - {\text{2)}}}}} \right|$
While solving the above we get,
${\text{tan}}\theta = \left| {\dfrac{{\dfrac{3}{2}}}{2}} \right|$
The tangent angle between two medians is,
${\text{tan}}\theta = \left| {\dfrac{3}{4}} \right| = \dfrac{3}{4}$

Step 3
By the question, we have to find the cosine of the obtuse angle,

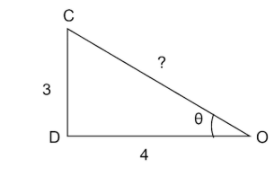
The above triangle is drawn by using ${\text{tan}}\theta = \dfrac{3}{4}$ since ${\text{tan}}\theta = \dfrac{{{\text{opposite side}}}}{{{\text{adjacent side}}}}$
By using the pythagoras theorem we will be able to find the third side of the above triangle,
${\text{O}}{{\text{C}}^2} = {\text{O}}{{\text{D}}^2}{\text{ + D}}{{\text{C}}^2}$
By substituting the values, we get,
${\text{O}}{{\text{C}}^2} = {4^2}{\text{ + }}{{\text{3}}^2}$
While solving the above we get,
${\text{O}}{{\text{C}}^2} = 16{\text{ + 9}}$
By adding we get.
${\text{O}}{{\text{C}}^2} = 25$
By solving we get,
${\text{OC}} = \sqrt {25}$
The third side(hypotenuse) of the above triangle will be,
${\text{OC}} = 5$
Then the cosine of the triangle will be,
${\text{cos}}\theta = \dfrac{{{\text{adjacent side}}}}{{{\text{hypotenuse}}}}$
By substituting the values, we get,
${\text{cos}}\theta = \dfrac{4}{5}$
But the angle formed by the cosine of the obtuse angle will be $\pi - \theta$
${\text{cos(}}\pi - \theta {\text{)}} = - \cos \theta$
By substituting the cos theta value, we get,
${\text{cos(}}\pi - \theta {\text{)}} = - \dfrac{4}{5}$
$\therefore$The required cosine angle of the obtuse angle is $- \dfrac{4}{5}$.
Hence, the cosine of the obtuse angle formed by medians drawn from the vertices of the acute angles of an isosceles right angled triangle is $- \dfrac{4}{5}$ .
Thus, the option $({\text{D}})$ is correct.

Note: The angle of any straight line will be ${180^ \circ }{\text{or }}\pi$. Since the medians drawn are straight lines, it forms an angle of ${180^ \circ }{\text{or }}\pi$ . That is the reason, we subtract $\pi$ and $\theta$ in the first triangle . The two medians intersect to form the centroid of the triangle.