Question
Question: The correct graph between the frequency \( 'n' \) and square root of density \( (\rho ) \) of a wire...
The correct graph between the frequency ′n′ and square root of density (ρ) of a wire, keeping its length, radius and tension constant is:
(A) 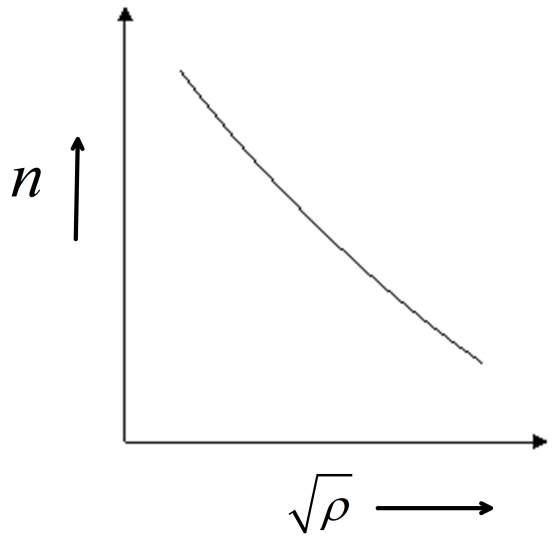
(B) 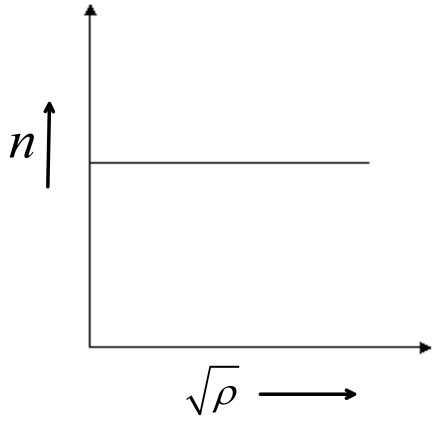
(C) 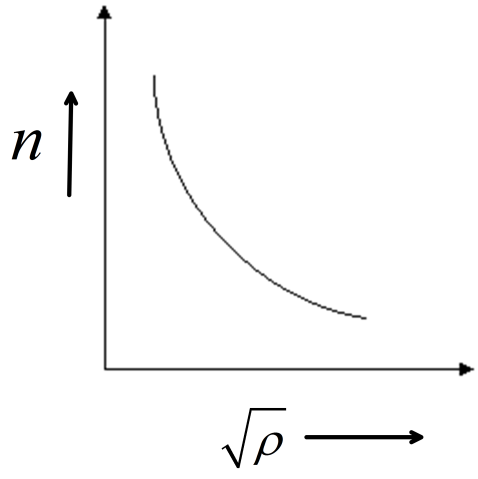
(D) 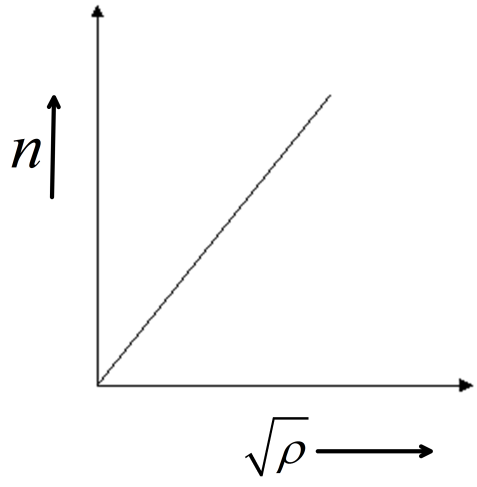
Solution
Hint : Observe the formula for frequency of transverse vibration in a stretched string. It is known that the frequency of p th harmonic of a transverse vibration in a stretched string is given by, n=2lpπr2ρT . Where, T is the tension of the stretched string, l is the length of the stretched string. r is the radius of the stretched string and ρ is the density of the stretched string material.
Complete Step By Step Answer:
We know that the, frequency of p th harmonic of a transverse vibration in a stretched string is given by, n=2lpπr2ρT . Where, T is the tension of the stretched string, l is the length of the stretched string. r is the radius of the stretched string and ρ is the density of the stretched string material.
So, if we keep the tension of the string, length of the string and radius of the stretched string then for say p th harmonic frequency of the string is related to density of the wire as, n=kρ1
where k is constant k=2lpπr2T .
So, we can write, n∝ρ1
So, frequency is inversely proportional to the square root of density of the material.
This signifies an equation of hyperbola. Hence, the plot between frequency of the string and the square root of density ρ will be hyperbolic.
Option (C ) signifies a graph of a hyperbola.
Hence, option (c ) is correct.
Note :
This relation between frequency of the stretched string and the square root of the density of the wire is known as the Law of density for transverse vibration in stretched string. It states that, if length, radius and tension of the wire is kept constant then frequency of transverse vibration will be inversely proportional to the square root of density of the wire.
