Question

The correct geometry and hybridization of ${\text{Xe}}{{\text{F}}_{\text{4}}}{\text{\;}}$ are:
A.Octahedral, $s{p^3}{d^2}$
B.Trigonal bipyramidal, $s{p^3}d$
C.Planar triangle, $s{p^3}{d^3}$
D.Square planar, $s{p^3}{d^2}$

Answer 1

To answer this question, you should recall that xenon is a noble gas and when bonding it will have the tendency to use all the eight electrons in the outermost shell to form bond pairs. We know fluorine is a halogen and can form one sigma bond with the central atom. Now, use this information to answer the question.

Complete step by step answer:
It is evident from the formula ${\text{Xe}}{{\text{F}}_{\text{4}}}$ that it is a ${\text{A}}{{\text{B}}_{\text{4}}}{{\text{L}}_{\text{2}}}$ type molecule where ${\text{A}}$ is the central atom and ${\text{L}}$ is the peripheral atom. Here, we can see that xenon is bonded with four fluorine atoms.
As we know that fluorine can form a single sigma bond, it will be bonded to ${\text{Xe}}$ with 4 sigma bonds. This leaves xenon with two lone pairs. To avoid repulsion and provide maximum stability, these lone pairs will be attached at an angle of $180^\circ$.
So, the hybridization of this molecule will be $s{p^3}{d^2}$. This means that geometry is octahedral and arrangement of electrons around the central atom is square planar due to the presence of two lone pair electrons.

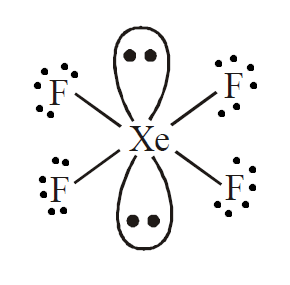
Therefore, we can conclude that the correct answer to this question is option D.

Note:
Even if you are not able to calculate the hybridisation using the above-mentioned, you can find the hybridization $X$ using the formula: $\dfrac{1}{2}\left( {V + H - C + A} \right)$ where,
$V$= Number of valence electrons in the central atom
$H$= Number of surrounding monovalent atoms
$C$= Cationic charge
$A$= Anionic charge
The value of $X$ will determine the hybridisation of the molecule. If $X = 2$, the hybridisation is $sp$. If $X = 3$, the hybridisation is $s{p^2}$. If $X = 4$, the hybridisation is $s{p^3}$; If $X = 5$, the hybridisation is $s{p^3}d$. If $X = 6$, the hybridisation is $s{p^3}{d^2}$. If $X = 7$, the hybridization is $s{p^3}{d^3}$.
Now, to determine the hybridization of ${\text{Xe}}{{\text{F}}_{\text{4}}}{\text{\;}}$.
Here, the total valence electrons, $V$ is 8 and the number of surrounding monovalent atoms, $H$ is 4. Cationic charge $C$ and anionic charge $A$ are 0.
Substituting in the formula we get,
$X = \dfrac{1}{2}\left( {8 + 4 - 0 + 0} \right) \\\ = \dfrac{1}{2}\left( {12} \right) \\\ = 6 \\\$
Thus, hybridization of ${\text{Xe}}{{\text{F}}_{\text{4}}}$ is $s{p^3}{d^2}$.