Question

The correct expression for Ampere’s law is:
A. $\int {B.dl = \sum i }$
B. $\int {B.dl = \dfrac{1}{{\sum i }}}$
C. $\int {B.dl = {\mu _0}\sum i }$
D. $\int {B.dl = \dfrac{{\sum i }}{{{\mu _0}}}}$

Answer 1

Early experimentations by scientists such as Maxwell and Oersted show that whenever there is an electric current, there is another invisible force acting on the metallic objects called magnetism. However, it was not until Jean Biot and Felix Savart in 1820, that this theory was confirmed. And alternatively, this was also confirmed by Ampere’s circuital law.

Complete step-by-step answer:
Biot Savart’s law gives us an insight about the term magnetic field that arises due to presence of electric current.
Consider a line element in a conductor $dl$ through which current is flowing and an arbitrary point P at a distance of r from the conductor

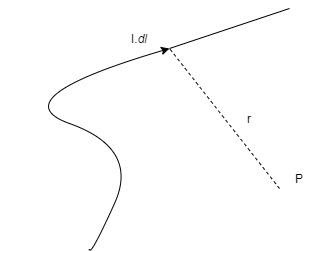
It states that, the magnetic field due to the line element $dl$is given by –
$dB \propto \dfrac{{I.dl}}{{{r^3}}}$
By removing the proportionality symbol, we have –
$dB = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I.dl}}{{{r^3}}}$ where ${\mu _0}$ is called the absolute permeability.
Another alternative for this law is the Ampere’s circuital law. The Ampere’s circuital law could be applied to surfaces with a boundary
Consider the surface with the boundary as shown.

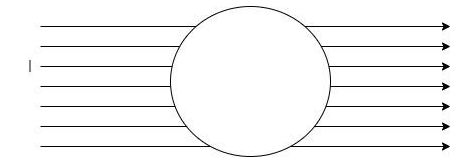
$I$ is the current flowing. Let $dl$ be the line element of the boundary.
By summing the line integrals infinistemally, we obtain a term known as line integral. So, the magnetic field associated with each line element $dl$ is summed up to form the line integral.
The Ampere’s circuital law states that this line integral of the magnetic field B over the entire boundary is equal to ${\mu _0}$ times the current flowing through it.
$\oint {B.dl = {\mu _0}} I$
Here, if $i$ is considered to be current through each line element, the total current will be equal to the summation of the current. Hence –
$\oint {B.dl = {\mu _0}} \sum i$

Hence, the correct option is Option C.

Note: Applying Biot-Savart’s Law and Ampere’s Circuital law over a boundary will result in the same expression for the magnetic field. The Ampere’s law is, however, very significant in electromagnetic radiation, wherein, a scientist by name James Maxwell, generalised this Ampere’s law equation to include in the list of his 4 fundamental Maxwell equations of classical electromagnetism.