Solveeit Logo
Login

Question

Question: The correct Biot-Savart law in vector form is? \[ A.{\text{ }}d\vec B = \dfrac{{{\mu _0}}}{{4\...

The correct Biot-Savart law in vector form is?

A. dB⃗=μ04πI(dl⃗×r⃗)r2 B. dB⃗=μ04πI(dl⃗×r⃗)r3 C. dB⃗=μ04πIdl⃗r2 D. dB⃗=μ04πIdl⃗r3  A.{\text{ }}d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I\left( {d\vec l \times \vec r} \right)}}{{{r^2}}} \\\ B.{\text{ }}d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I\left( {d\vec l \times \vec r} \right)}}{{{r^3}}} \\\ C.{\text{ }}d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Id\vec l}}{{{r^2}}} \\\ D.{\text{ }}d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Id\vec l}}{{{r^3}}} \\\
Explanation

Solution

- Hint: In order to deal with this question first we will understand the Biot-Savart law, then we will proceed further by considering the Biot-Savart law formula and by changing it in vector form we will get the answer.

Formula used- dB⃗=μ04πIdlsin⁡θr2r^,r^=r⃗rd\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Idl\sin \theta }}{{{r^2}}}\hat r,\hat r = \dfrac{{\vec r}}{r}

Complete step-by-step solution -
Biot-Savart's law: Biot-Savart's law is an equation that gives the magnetic field generated as a result of an actual section of carrying. This section is taken as the sum of a vector known as the current dimension.
Figure:

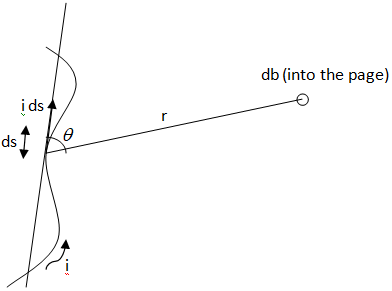
Biot-Savart’s law formula: Consider a current carrying wire II in a specific direction as shown in the above figure. Consider a small length element in the given wire of length dldl . We know that the direction of this current element will be the same as that of the current so that it forms a vector Idl⃗Id\vec l .
To know the magnetic field generated at a time because of this small part, Biot-Savart's law can be applied. Let the position vector of the point in question drawn from the current element be r and the angle between the two be θ\theta . Then,
dB⃗=μ04πIdlsin⁡θr2r^d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Idl\sin \theta }}{{{r^2}}}\hat r
Where
μ0{\mu _0} is the permeability of free space and is equal to 4π×10−7TmA−14\pi \times {10^{ - 7}}Tm{A^{ - 1}} .
So the Biot Savart's Law formula is
Now we know:
r^=r⃗r\hat r = \dfrac{{\vec r}}{r}
Using this and the cross product of two vectors we get;
∵dB⃗=μ04πIdlsin⁡θr2r^ ⇒dB⃗=μ04πIdl⃗sin⁡θr2r⃗r ⇒dB⃗=μ04πI(dl⃗.r⃗sin⁡θ)r2×r ⇒dB⃗=μ04πI(dl⃗×r⃗)r3 [∵a⃗×b⃗=absin⁡θ]  \because d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Idl\sin \theta }}{{{r^2}}}\hat r \\\ \Rightarrow d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Id\vec l\sin \theta }}{{{r^2}}}\dfrac{{\vec r}}{r} \\\ \Rightarrow d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I\left( {d\vec l.\vec r\sin \theta } \right)}}{{{r^2} \times r}} \\\ \Rightarrow d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I\left( {d\vec l \times \vec r} \right)}}{{{r^3}}}{\text{ }}\left[ {\because \vec a \times \vec b = ab\sin \theta } \right] \\\
Hence, the correct Biot-Savart law in vector form is dB⃗=μ04πI(dl⃗×r⃗)r3d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I\left( {d\vec l \times \vec r} \right)}}{{{r^3}}}
Hence the correct answer is option B.

Note- The Biot – Savart law is a general law in electromagnetism which describes the magnetic field that has been generated by a steady electric current. This links the magnetic field to the amplitude, distance, length and closeness of electric current. We may also use the Biot – Savart theorem for calculating magnetic reactions at the atomic or molecular level. This is often used in aerodynamic theory to calculate the displacement induced by the vortex shapes.