Question

The coordinates of the point that is two thirds away from (-4, 3) to (5, 7) is
A. $\left( \dfrac{17}{2},3 \right)$
B. $\left( 2,\dfrac{17}{3} \right)$
C. $\left( 2,\dfrac{3}{17} \right)$
D. $\left( 3,\dfrac{2}{17} \right)$

Answer 1

In order to solve this question, we should know the section formula, that is , if a point, $\left( x,y \right)$ divides a line joining $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio $m:n$, then $x=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$ and $y=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$. By using this concept, we can solve this question.

Complete step by step answer:
In this question, we have been asked to find the coordinates of the point which is two-thirds away from (-4, 3) to (5, 7). Now let us consider the point which is two thirds away from (-4, 3) to (5, 7) to be $\left( x,y \right)$. So, we can say that $\left( x,y \right)$ is two third away from (-4, 3) to (5, 7). Now if we consider the length of the points (-4, 3) to (5, 7) to be L, then length from (-4, 3) to $\left( x,y \right)$ will become $\dfrac{2}{3}L$, because $\left( x,y \right)$ is two thirds away from (-4, 3) to (5, 7). So, the length of $\left( x,y \right)$ to (5, 7) will become $L-\dfrac{2L}{3}=\dfrac{L}{3}$. Therefore we can say $\left( x,y \right)$ is intersecting (-4, 3) and (5, 7) in the ratio of $\left( \dfrac{2}{3}:\dfrac{1}{3} \right)$ which is the same as (2 : 1). Hence, to find the value of $\left( x,y \right)$, we will apply section formula, which states that if a point, $\left( x,y \right)$ divides a line joining $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio $m:n$, then $x=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$ and $y=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$.

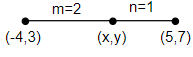
So, for the values of m = 2 and n = 1 and $\left( {{x}_{1}},{{y}_{1}} \right)$ as (-4, 3) and $\left( {{x}_{2}},{{y}_{2}} \right)$ as (5, 7), we can write the values of x, y as,
$x=\dfrac{2\times 5+1\times \left( -4 \right)}{2+1}$ and $y=\dfrac{2\times 7+1\times 3}{2+1}$
Now, we will simplify it further to get the value of x and y. So, we get,
$\begin{aligned} & x=\dfrac{10-4}{3}\text{ }and\text{ }y=\dfrac{14+3}{3} \\\ & \Rightarrow x=\dfrac{6}{3}\text{ }and\text{ }y=\dfrac{17}{3} \\\ & \Rightarrow x=2\text{ }and\text{ }y=\dfrac{17}{3} \\\ \end{aligned}$
Hence, we get the coordinates of the point, that is two third away from (-4, 3) to (5, 7) is $\left( x,y \right)$ as $\left( 2,\dfrac{3}{17} \right)$. Therefore, option B is the correct answer.

Note: While solving this question, the possible mistakes we can make is to consider $\dfrac{2}{3}$ as 2 : 3 = m : n, which would be totally incorrect. Here, the word two thirds represents that if the length of the segment is three, then $\left( x,y \right)$ is 2 units away from (-4, 3) in the direction of (5, 7).