Question

The coordinates of the image of the origin O with respect to the line $x + y + 1 = 0$ are
A. $\left( { - \dfrac{1}{2}, - \dfrac{1}{2}} \right)$
B. $\left( { - 2, - 2} \right)$
C. $\left( {1,1} \right)$
D. $\left( { - 1, - 1} \right)$

Answer 1

First we will first assume that $Q\left( {h,k} \right)$ be the image of $O\left( {0,0} \right)$ with respect to the line $x + y + 1 = 0$ and then use the formula to point image of the origin to the line is $\dfrac{{h - 0}}{a} = \dfrac{{k - 0}}{b} = - 2\dfrac{c}{{\sqrt {{a^2} + {b^2}} }}$, where $ax + by + c = 0$ is the line.

Complete step by step Answer:

We are given that the coordinates of the image of the origin O with respect to the line $x + y + 1 = 0$.

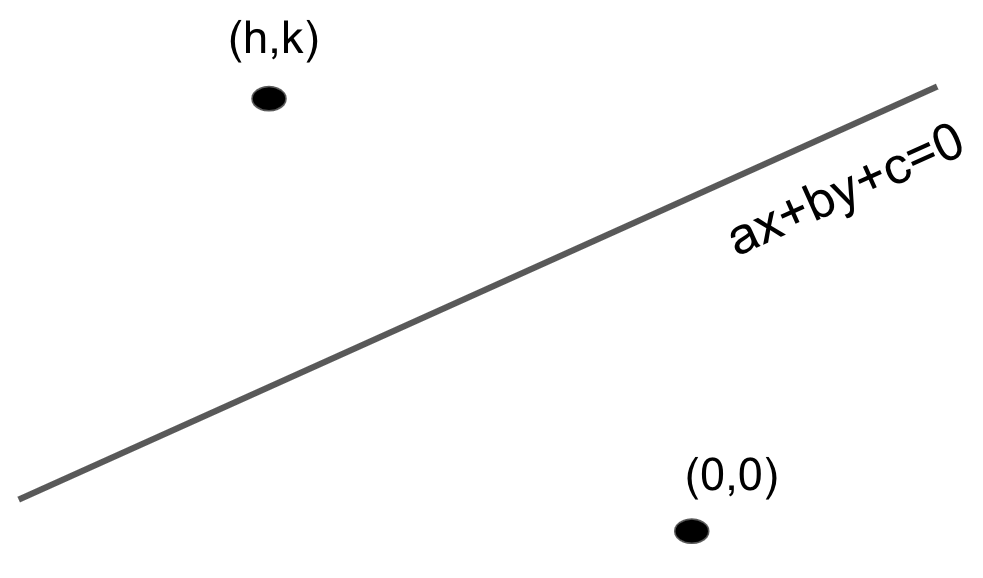
Let us assume that $Q\left( {h,k} \right)$ be the image of $O\left( {0,0} \right)$ with respect to the line $x + y + 1 = 0$.

We know that the formula to find the image of the origin to the line is $\dfrac{{h - 0}}{a} = \dfrac{{k - 0}}{b} = - 2\dfrac{c}{{\sqrt {{a^2} + {b^2}} }}$, where $ax + by + c = 0$ is the line.

Finding the value of $h$and $k$ from the above assumption, we get

$$\Rightarrow \dfrac{{h - 0}}{1} = \dfrac{{k - 0}}{1} = \dfrac{{ - 2\left( 1 \right)}}{1} \\\ \Rightarrow h = k = - 1 \\\$$

$\Rightarrow h = - 1$, $k = - 1$

So, the image is at $\left( { - 1, - 1} \right)$.
Hence, option D is correct.

Note: In solving this type of question, we can also solve this by finding the midpoint and then finding the equation and slope of normal, which is a long process so we adopt the above method. The key concept is to remember the formula to find the image of the point to the line. One should take care of the signs of the required value.