Question
Question: The coordinates of the foci of the hyperbola xy = c² are...
The coordinates of the foci of the hyperbola xy = c² are
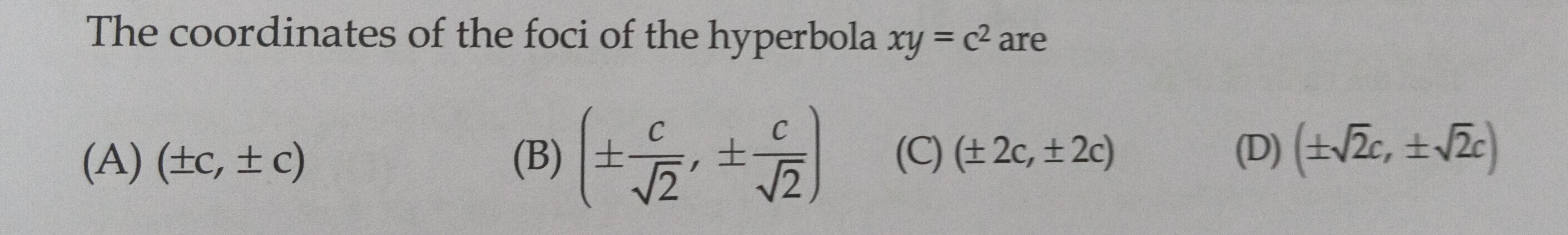
(±c, ± c)
(±2c, ±2c)
(±2c, ±2c)
(±2c, ±2c)
(±2c, ±2c)
Solution
The given equation of the hyperbola is xy=c2. This is a rectangular hyperbola whose asymptotes are the coordinate axes.
To find the foci, we can rotate the coordinate axes by an angle of 45∘. Let the new coordinates be (X,Y). The transformation equations are:
x=Xcos45∘−Ysin45∘=X21−Y21=2X−Y
y=Xsin45∘+Ycos45∘=X21+Y21=2X+Y
Substitute these into the equation xy=c2:
(2X−Y)(2X+Y)=c2
2X2−Y2=c2
X2−Y2=2c2
2c2X2−2c2Y2=1
This is the standard form of a hyperbola a2X2−b2Y2=1, where a2=2c2 and b2=2c2.
For this hyperbola in the (X,Y) system:
The semi-major axis is a=2c2=2∣c∣. We can assume c>0 without loss of generality for finding coordinates, the ± signs will handle the case c<0. So a=2c.
The semi-minor axis is b=2c2=2c.
The eccentricity e is given by e2=1+a2b2.
e2=1+2c22c2=1+1=2
e=2 (since eccentricity is always positive).
The foci of the hyperbola a2X2−b2Y2=1 in the (X,Y) system are located at (±ae,0).
Foci in (X,Y) are (±(2c)(2),0)=(±2c,0).
The two foci are (2c,0) and (−2c,0) in the (X,Y) system.
Now we need to convert these coordinates back to the original (x,y) system using the inverse transformation equations:
x=2X−Y
y=2X+Y
For the focus (X,Y)=(2c,0):
x=22c−0=22c=2c
y=22c+0=22c=2c
So, one focus is (2c,2c).
For the focus (X,Y)=(−2c,0):
x=2−2c−0=2−2c=−2c
y=2−2c+0=2−2c=−2c
So, the other focus is (−2c,−2c).
The coordinates of the foci are (2c,2c) and (−2c,−2c).
This set of points can be represented as (±2c,±2c), where the signs are taken together (i.e., (+,+) and (−,−)).
