Question

The coordinates of the centre of mass of a uniform flag shaped lamina (thin flat plate) of mass 4kg. (The coordinates of the same are shown in figure) are:

1. $(1.25m,1.50m)$
2. $(1m,1.75m)$
3. $(0.75m,0.75m)$
4. $(0.75m,1.75m)$

Answer 1

It is an imaginary point at which the whole mass of a body is supposed to be concentrated called the centre of mass and the concept of the centre of mass is that of the product of the masses by their distance from a reference point.

Complete step by step solution:
Given that the mass of uniform flag lamina is = $4Kg$
Now, we know that the lamina means (thin flat plate),

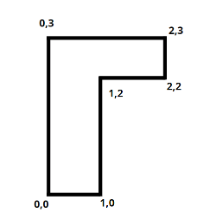
According to the diagram, Lamina can be considered into two rectangular parts and the two parts A and B having masses of $2Kg$ for A and $2Kg$ for B.
Mass of part A is given by

$\begin{gathered} {m_A} = \sigma \times {A_A} \\\ = \sigma \times 2 \times 1 \\\ \end{gathered}$

$= 2\sigma$................( 1)

Similarly, Mass of part B is given by

$\begin{gathered} {m_B} = \sigma \times {A_B} \\\ = \sigma \times 1 \times 2 \\\ \end{gathered}$
$= 2\sigma$.....................( 2)

Coordinate of the center of masses of the parts are given by
$\begin{gathered} {X_{A(c.o.m)}} = \frac{{{x_1} + {x_2}}}{2} \\\ {Y_{A(c.o.m)}} = \frac{{{y_1} + {y_2}}}{2} \\\ \end{gathered}$ and

For part A is given by,

${X_{A(c.o.m)}} = \dfrac{{0 + 2}}{2} = 1$ …………...(3)
${Y_{A(c.o.m}} = \dfrac{{2 + 3}}{2} = \dfrac{5}{2}$..................(4)

For part B is given by

${X_{B(c.o.m)}} = \dfrac{{0 + 1}}{2} = \dfrac{1}{2}$ ……………..(5)
${Y_{B(c.o.m)}} = \dfrac{{2 + 0}}{2} = 1$.........................(6)

Now combining part A and part B,
According to the formula of center of mass

${X_{c.o.m}} = \dfrac{{{m_A}{X_A} + {m_B}{X_B}}}{{{m_A} + {m_B}}}$ (Equation 7)

Putting the value of equation (1), (3) and (5) in equation (7)
We get,

$\begin{gathered} = \frac{{2\sigma (1) + 2\sigma (\frac{1}{2})}}{{2\sigma + 2\sigma }} \\\ = \frac{{3\sigma }}{{4\sigma }} \\\ = \frac{3}{4} \\\ \end{gathered}$

Similarly,

${Y_{c.o.m}} = \dfrac{{{m_A}{Y_A} + {m_B}{Y_B}}}{{{m_A} + {m_B}}}$
$\begin{gathered} = \dfrac{{2\sigma (\dfrac{5}{2}) + 2\sigma (1)}}{{2\sigma + 2\sigma }} \\\ = \dfrac{{7\sigma }}{{4\sigma }} \\\ = \frac{7}{4} \\\ \end{gathered}$

The required coordinate of this system is given by $(\dfrac{3}{4},\dfrac{7}{4})$ and in decimals $(0.75,1.75)$

Hence, Option 4 is the correct answer.

Note: Remember, the location of mass depends on the distribution of masses and their individual location in the system and for regular geometrical shaped bodies having a uniform distribution of mass located at their centre.