Question
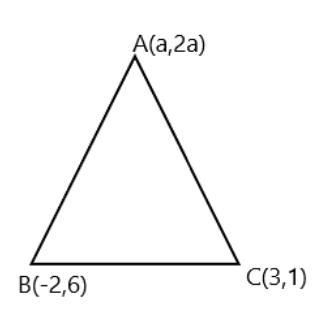
Question: The coordinates of A for which area of triangle, whose vertices are \( A(a,2a),B( - 2,6) \) and \( C...
The coordinates of A for which area of triangle, whose vertices are A(a,2a),B(−2,6) and C(3,1) is 10 square units are:
A. (0,3)
B. (5,8)
C. (3,38)
D. None of these
Solution
Hint : As we know that the above question is related to the coordinate geometry. We know the formula of area of triangle is 21[a1(b1−b2)+b1(c1−c2)+c1(a1−a2)] , where [(b1−b2),(c1−c2)and(a1−a2)] are the coordinates of vertices of triangle. We will apply this formula of area of the triangle and find the value of a .
Complete step by step solution:
Here in this question, the area is 10 square units. We have
a1=a,a2=2a,b1=−2,b2=6 and c1=3 , c2=1 .
Are of triangle is
21[a1(b1−b2)+b1(c1−c2)+c1(a1−a2)] , by putting the values we have:
10=21[a(−2−6)+(−2)(3−1)+3(a−2a)] .
We will now solve it,
−8a−4−3a=20 ⇒−11a=24
On further solving we have a=−1124 and then 2a=2×−1124=−1148 .
Hence the correct option is (D).
So, the correct answer is “Option D”.
Note : Before solving this kind of question we should have the proper knowledge of triangles, their area and the vertices. Sometimes we get a quadratic equation while finding the value of required missing number, then we can find the value of roots by the method of quadratic formula i.e. 2a−b±b2−4ac .
