Solveeit Logo
Login

Question

Question: The coordinates of A, B, C are \[\left( {6,3} \right),\left( { - 3,5} \right),\left( {4, - 2} \right...

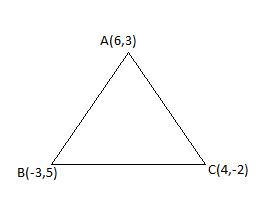
The coordinates of A, B, C are (6,3),(−3,5),(4,−2)\left( {6,3} \right),\left( { - 3,5} \right),\left( {4, - 2} \right)respectively and P is any point (x,y)\left( {x,y} \right). Show that the ratio of area of ∆PBC to that of ∆ABC is ∣x+y−2∣7\dfrac{{\left| {x + y - 2} \right|}}{7}.

Explanation

Solution

Here we are given coordinates of vertices of ∆ABC along with coordinates of point P. Since we are not given the height of the triangle we will use the formula given below to find the area of both the triangles.

Formula used:

Area of the triangle with coordinates (x1,y1),(x2,y2),(x3,y3)\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right) is given by,
⇒12∣x1(y2−y3)+x2(y3−y1)+x3(y1−y2)∣\Rightarrow \dfrac{1}{2}\left| {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right|

Complete step-by-step answer:
For ∆ABC, coordinates are A (x1,y1)\left( {{x_1},{y_1}} \right)=(6,3)\left( {6,3} \right) , B (x2,y2)\left( {{x_2},{y_2}} \right)=(−3,5)\left( { - 3,5} \right) , C (x3,y3)\left( {{x_3},{y_3}} \right)=(4,−2)\left( {4, - 2} \right).
Area of ∆ABC ⇒12∣x1(y2−y3)+x2(y3−y1)+x3(y1−y2)∣ \Rightarrow \dfrac{1}{2}\left| {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right|
Substituting the values

⇒12∣6(5−(−2))+(−3)(−2−3)+4(3−5)∣ ⇒12∣6×7+(−3)(−5)+4×(−2)∣ ⇒12∣42+15−8∣ ⇒12∣49∣  \Rightarrow \dfrac{1}{2}\left| {6\left( {5 - \left( { - 2} \right)} \right) + ( - 3)\left( { - 2 - 3} \right) + 4\left( {3 - 5} \right)} \right| \\\ \Rightarrow \dfrac{1}{2}\left| {6 \times 7 + ( - 3)( - 5) + 4 \times ( - 2)} \right| \\\ \Rightarrow \dfrac{1}{2}\left| {42 + 15 - 8} \right| \\\ \Rightarrow \dfrac{1}{2}\left| {49} \right| \\\

⇒492 \Rightarrow \dfrac{{49}}{2}

For ∆PBC, coordinates are P(x,y)=(x1,y1)P\left( {x,y} \right) = \left( {{x_1},{y_1}} \right), B(x2,y2)=(−3,5),C(x3,y3)=(4,−2)B\left( {{x_2},{y_2}} \right) = \left( { - 3,5} \right),C\left( {{x_3},{y_3}} \right) = \left( {4, - 2} \right)
Area of ∆PBC ⇒12∣x1(y2−y3)+x2(y3−y1)+x3(y1−y2)∣ \Rightarrow \dfrac{1}{2}\left| {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right|
Substituting the values

⇒12∣x(5−(−2))+(−3)(−2−y)+4(y−5)∣ ⇒12∣7x+6+3y+4y−20∣ ⇒12∣7x+7y−14∣  \Rightarrow \dfrac{1}{2}\left| {x\left( {5 - \left( { - 2} \right)} \right) + ( - 3)\left( { - 2 - y} \right) + 4\left( {y - 5} \right)} \right| \\\ \Rightarrow \dfrac{1}{2}\left| {7x + 6 + 3y + 4y - 20} \right| \\\ \Rightarrow \dfrac{1}{2}\left| {7x + 7y - 14} \right| \\\

Taking 7 common
⇒72∣x+y−2∣\Rightarrow \dfrac{7}{2}\left| {x + y - 2} \right|
Now we have to take ratio of area of ∆PBC to ∆ABC

⇒Area(△PBC)Area(△ABC) ⇒72∣x+y−2∣492 ⇒∣x+y−2∣7  \Rightarrow \dfrac{{Area\left( {\vartriangle PBC} \right)}}{{Area\left( {\vartriangle ABC} \right)}} \\\ \Rightarrow \dfrac{{\dfrac{7}{2}\left| {x + y - 2} \right|}}{{\dfrac{{49}}{2}}} \\\ \Rightarrow \dfrac{{\left| {x + y - 2} \right|}}{7} \\\

This is the ratio so obtained.
Hence proved.

Note: Don’t use any other formula to find the area here because we are given the coordinates only. Also find the values of modulus. Take the correct ratio of areas of triangles. Carefully add and subtract the signs.