Question
Question: The connections shown in figure are established with the switch S open. Charge flow through the swit...
The connections shown in figure are established with the switch S open. Charge flow through the switch if it is closed is 1.2×10−xC. Find the value of x.
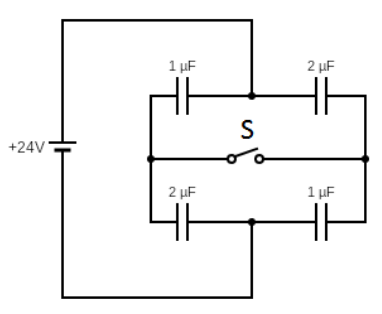
Solution
Find the total charge in the equivalent capacitor when switch is open and calculate the potential at the junction of switch then calculate charge flowing through the junction. Equivalent capacitance of capacitors connected in parallel is given by, Ceq1=C11+C21+C31+.... The total charge on a capacitor of capacitance Cis q=CV where V is the voltage across the capacitor.
Complete step by step answer:
Here the switch is opened at first. So, let’s find the total charge on the circuit when the switch is opened. So, we can draw the circuit as follows.
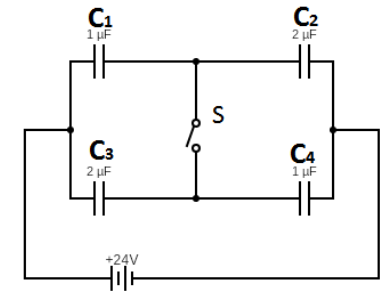
We know the, Equivalent capacitance of capacitors connected in parallel is given by, Ceq1=C11+C21+C31+...
Now, the equivalent capacitance of the C1=1μFand C2=2μF will be,
Ceq11=C11+C21=11+21=23
⇒Ceq1=32μF
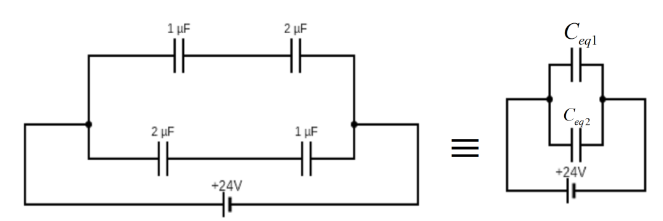
Similarly, the equivalent capacitance of the C3=2μF and C4=1μF will be,
Ceq2=32μF
Now, the voltage across the two branches is the same. Hence, they will carry the same charge at open condition. Hence, the charge at C1 and C4 will be the same and similarly charge at C2 and C3 will be the same. When the switch is just closed the potential on the switch junction will become the same in a certain time. And charge on C1 and C4 will be same when the switch is just closed, similarly charge C2 in and C3 will be same. After that they will start discharging due to voltage difference and finally make the voltage at the switch junction same.
Let, the potential at the junction is V0. So, we can write, QC1=QC4.Putting the value we get,
1×(24−V0)=1×V0
⇒V0=12
Hence, for closed condition the charge on C1 will be, QC1=1×12=12μC.
Charge on C2 will be, QC2=2×12=24μC
Now, the charge flowing through the junction is q.
Hence, we can write, QC2=q+QC1.
Putting the values we get, q=24−12=12μC.
So, equating this with given charge we get,
1.2×10−x=12×10−6
⇒10−x=10−5
∴x=5
Hence, the value of x is 5.
Note: When the circuit is closed the charge q=1.2×10−5 will flow producing current in the circuit for a certain time until the potential in the junction of the switch is the same. When the capacitors are charged again and potential becomes V0 the current will stop. Equivalent capacitance of capacitors connected in series is given by, Ceq=C1+C2+C3+...
