Question

The connections shown in figure are established with the switch $S$ open. The charge which flows. Through the switch if it is closed is.

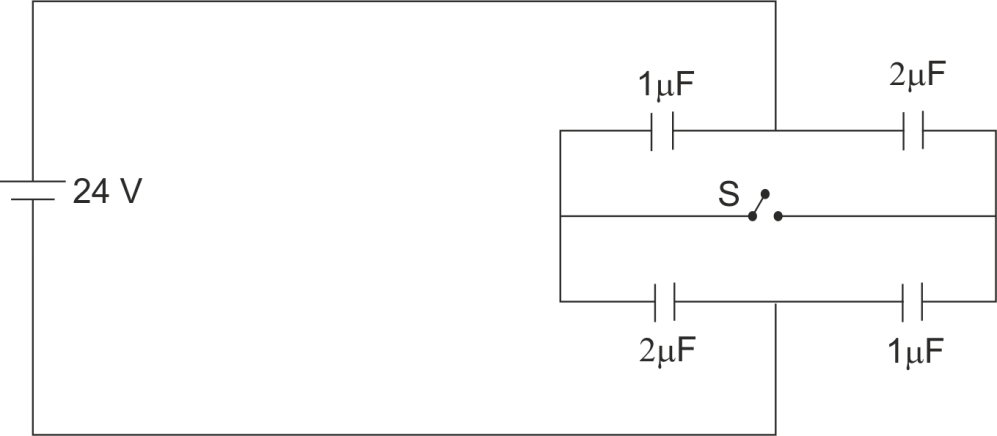
(a) $40\mu C$
(b) $30\mu C$
(c) $20\mu C$
(d) $12\mu C$

Answer 1

Hint : The flows of charge in an electric circuit signifies. The existence of electric current in that circuit. We can define electric current as the flow of electric charges in a conductor.
When charge flows through the open switch the circuit will not reach or it is an incomplete connection.
When charge is how through the close switch the circuit will react or it is complete connection.
Formula:- We fuse the capacitor formula.
${{C}_{eq}}={{\left( {{C}_{1}}+\dfrac{{{C}_{1}}}{{{C}_{2}}} \right)}^{-1}}+{{\left( \dfrac{{{C}_{4}}}{{{C}_{3}}}+{{C}_{4}} \right)}^{-1}}$
$Q={{C}_{eq}}.V$
Where
$Q=$ charge
$V=$ voltage
${{C}_{eq}}=$ equivalent capacitor .

Complete Step By Step Answer:
Capacitor given
${{C}_{1}}=1\mu F$
${{C}_{2}}=2\mu F$
${{C}_{3}}=2\mu F$
${{C}_{4}}=1\mu F$
$V=24V$
${{C}_{eq}}={{\left( 1+\dfrac{1}{2} \right)}^{-1}}+{{\left( \dfrac{1}{2}+1 \right)}^{-1}}$
$=\dfrac{2}{3}+\dfrac{2}{3}=\dfrac{4}{3}\mu F$
So, $Q={{C}_{eq}}.V=\dfrac{4}{3}\times 24=32\mu F$
This will be divided equally, as the capacitor are equal $\Rightarrow Q=16\mu F$

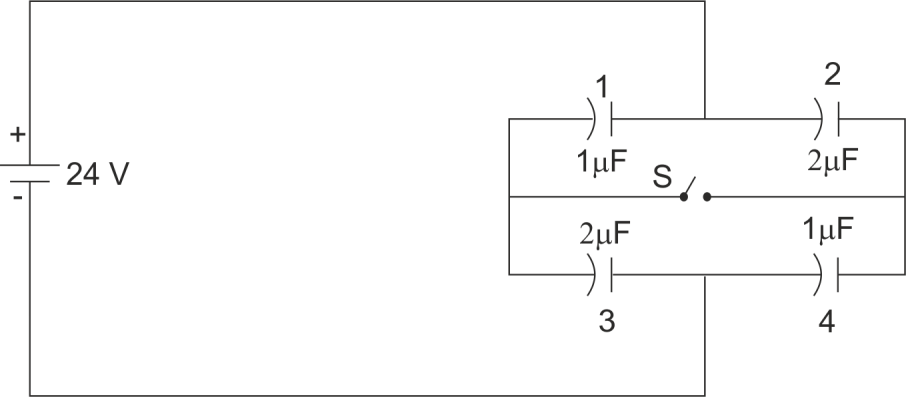
(a)

(b)
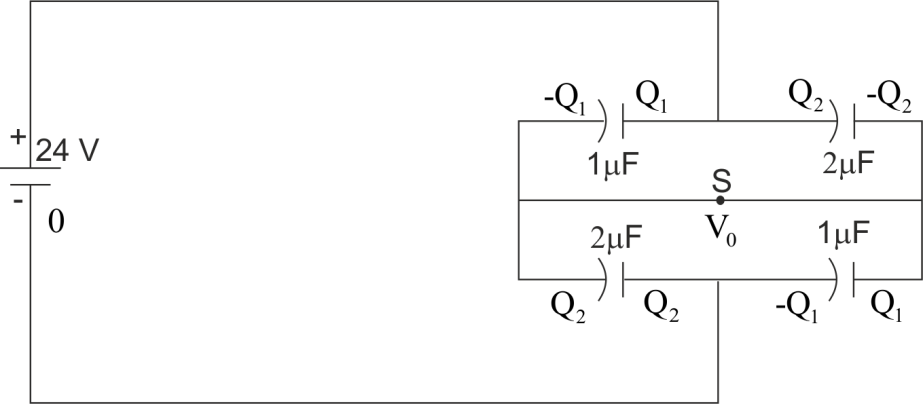
When the switch $S$ is closed as shown in the figure (b), then the charges stored across positive plates capacitor $1$ and be ${{Q}_{1}}\And {{Q}_{2}}$ The same charges will be distributed across negative plates of capacitor $3$ and $4$ Let potential at the negative terminal is zero then the charge across capacitor $1,2,3$ and will be.
${{Q}_{1}}=\left( 24-{{V}_{0}} \right)\times 1\mu F.....(a)$
${{Q}_{2}}=\left( 24-{{V}_{0}} \right)\times 2\mu F...(b)$
${{Q}_{3}}={{V}_{0}}\times 1\mu F...(c)$
${{Q}_{4}}={{V}_{0}}\times 1\mu F...(d)$
Thus from $(a)$ and $(d)$ ${{V}_{0}}=12V$ and thus the charges be: ${{Q}_{1}}={{Q}_{4}}=12\mu F\And {{Q}_{2}}={{Q}_{3}}=24\mu F$
In conclusion,
Thus when the switch is zero, $12\mu F$ charge is passed through the switch.

Additional Information:
In this question we used the capacitor formula and found the state at which switch is closed and with value of charges which will flow through the closed switch by using formula.

Note :
Capacitance is the ratio of the amount of electric charge stored on a conductor to a difference in electric potential. There are two closely related motions of capacitance: self-capacitance and mutual capacitance.