Question

The complete solution set of 12x + 11 - 15x - 21 > 1, is

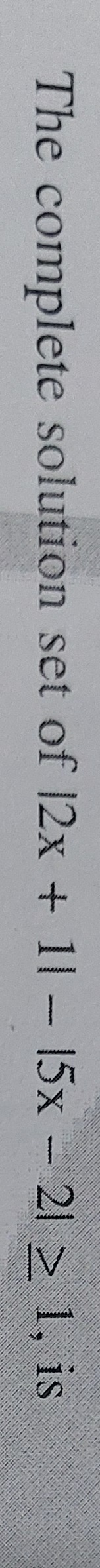
Answer 1

(-\infty, -\frac{11}{3})

Answer 2

The given inequality is $12x + 11 - 15x - 21 > 1$.

Combine the like terms on the left side: $(12x - 15x) + (11 - 21) > 1$ $-3x - 10 > 1$

Add 10 to both sides of the inequality: $-3x - 10 + 10 > 1 + 10$ $-3x > 11$

Divide both sides by -3. Remember to reverse the inequality sign because we are dividing by a negative number: $\frac{-3x}{-3} < \frac{11}{-3}$ $x < -\frac{11}{3}$

The complete solution set consists of all real numbers $x$ that are strictly less than $-\frac{11}{3}$. In interval notation, this is $(-\infty, -\frac{11}{3})$. In set-builder notation, this is $\{x \in \mathbb{R} \mid x < -\frac{11}{3}\}$.