Question
Question: The compensated pendulum of a clock consists of an isosceles triangular frame of base length \[{l_1}...
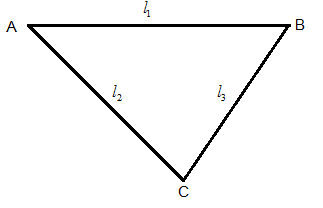
The compensated pendulum of a clock consists of an isosceles triangular frame of base length l1 and expansivity α1 and slides of length l2 and expansivity α2. The pendulum is supported, as shown in Figure. Find the ratio l2l1 so that the length of the pendulum may remain unchanged at all temperatures.
A. l2l1=2a1a2
B. l2l1=a1a2
C. l2l1=2a1a2
D. l2l1=a12a2
Solution
Three basic thermal expansions are linear expansion, superficial expansion and cubical expansion. Here, in the question we need to determine the ratio l2l1 so that the length of the pendulum may remain unchanged at all temperatures. For this the amount a material expands or contracts per unit length due to a one-degree change in temperature.
Complete step by step answer:
Let C be the base of the triangle,
Now draw a perpendicular bisector on the side AB from the vertex C
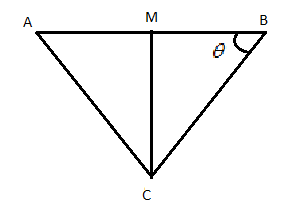
Here cosθ=BCBM=BC21BM=2l2l1
Now when the triangle expands,
Let A’B’C be the new triangle and draw a perpendicular AN from A to A’C
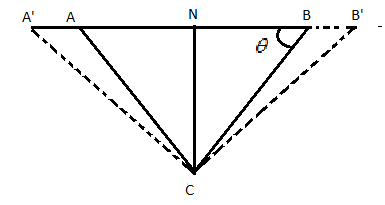
Here AA’=x increase in the length of AB=21l1α1t, where t is the increase in temperature and
A’N= increase in the length of AB=l2α2t
Since the change in angle after the expansion is very small, hence we can write
∠BAC=∠B′A′C=θ
Hence
cosθ=AA′A′N−−(i)
Where cosθ=2l2l1
Hence substituting the value in equation (i), we get
2l2l1=21l1α1tl2α2t
By solving
Hence the ratio l2l1so that the length of the pendulum may remain unchanged at all temperatures =2α1α2
So, the correct answer is “Option A”.
Note:
Expansion corresponds to change in length, area and volume of the substance where linear expansivity is the increase in the length of a substance for per unit length of the substance for one degree Celsius rise in temperature.
