Question

The compass needle of an airplane shows that it is heading towards the north and the speedometer measures the velocity of $240 kmh^{-1}$. Wind is blowing at $100 kmh^{-1}$ due east. Find the velocity of the airplane with respect to earth.
A) $260 kmh^{-1}, {23^0}$ east of north
B) $260 kmh^{-1}, {32^0}$ west of north
C) $260 kmh^{-1}, {23^0}$ west of north
D) None of these

Answer 1

The above problem is based on the vector subtraction and relative velocity concept. Airplane is heading towards north and wind is blowing towards east which means that velocity of airplane with respect to ground can be calculated by subtracting magnitude of velocity shown by speedometer and velocity of wind. Let’s get started with the vector subtraction to find out the speed of the plane with respect to round.

Complete step by step solution:
First let’s discuss vectors and relative velocity concepts in detail.
Vectors quantities are those which are characterised by both magnitude and direction. Vectors are represented by a line with an arrow head (which represents the direction of the vector).
Vector subtraction: The process of subtraction of one algebraic quantity from another is equivalent to adding the negative of the quantity to be subtracted.

The relative velocity is the velocity of an object or observer B in the rest frame of another object or observer A. Now, we calculate the velocity of the plane with respect to ground.

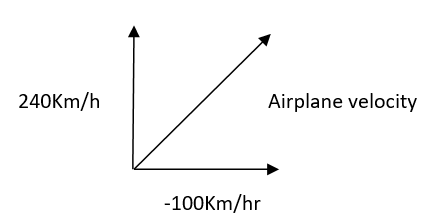
We will do vector subtraction by using the concept of Pythagoras theorem.
Velocity of an airplane will be denoted by $V_{ag}$ velocity of wind is $V_W$ and velocity of airplane $V_a$.
$\Rightarrow {V^2}_{ag} = {V_a}^2 + {V_w}^2 \\\ \Rightarrow {V_{ag}} = \sqrt {{V_a}^2 + {V_w}^2} \\\ \Rightarrow {V_{ag}} = \sqrt {{{(240)}^2} + {{(100)}^2}} \\\$ (We have used the formula and substituted the value of velocities)
$\Rightarrow {V_{ag}} = \sqrt {67600} \\\ \Rightarrow {V_{ag}} = 260Km/hr \\\$ (We have done the square and added the value)
To find the angle of movement of airplane we will use
$\Rightarrow \tan \theta = \dfrac{{{V_w}}}{{{V_a}}} \\\ \Rightarrow \tan \theta = \dfrac{{100}}{{240}} \\\$ (We have use the tangent formula)
$\Rightarrow \theta = {\tan ^{ - 1}}\dfrac{{100}}{{240}} \\\ \Rightarrow \theta = 22.67 \\\ \Rightarrow \theta = {23^0} \\\$
Option (A) is correct.

Note: Vector addition and subtraction can be done using two laws which are: parallelogram law of vector addition and triangle law of vector addition. In the triangle law of vector addition, the head of one vector is attached to the tail of another vector.