Question

The common tangents to the circle 2x² + 2y² = 1 and the parabola y² = 4x touch the circle at points P and Q and the parabola at points R and S. The area of the quadrilateral PQRS is $\frac{\alpha}{\beta}$, then $\alpha + \beta$ is equal to (where $\alpha$ and $\beta$ are coprime positive integers) _______.

Answer 1

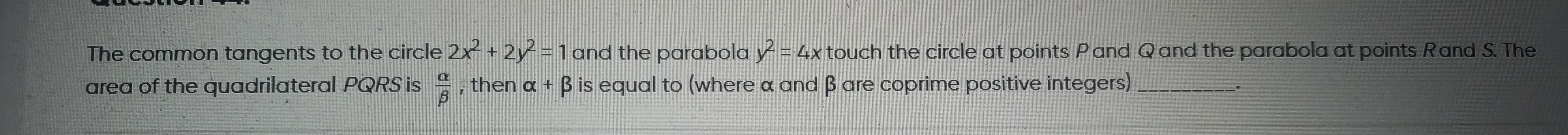
19

Answer 2

1. Standardize the Equations of the Curves: The given circle equation is $2x^2 + 2y^2 = 1$. Dividing by 2, we get $x^2 + y^2 = \frac{1}{2}$. This is a circle centered at the origin $(0,0)$ with radius $r = \frac{1}{\sqrt{2}}$. The given parabola equation is $y^2 = 4x$. This is a parabola opening to the right, with vertex at $(0,0)$ and parameter $a=1$ (from $y^2 = 4ax$).

2. Find the Equation of the Common Tangents: The general equation of a tangent to the parabola $y^2 = 4ax$ is $y = mx + \frac{a}{m}$. For $y^2 = 4x$, we have $a=1$, so the tangent equation is $y = mx + \frac{1}{m}$. Rearranging this into the standard form $Ax+By+C=0$, we get $m^2x - my + 1 = 0$.

For this line to be tangent to the circle $x^2 + y^2 = r^2$, the perpendicular distance from the center $(0,0)$ to the line must be equal to the radius $r$. Here, $r = \frac{1}{\sqrt{2}}$. The distance formula is $\frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}$. $\frac{|m^2(0) - m(0) + 1|}{\sqrt{(m^2)^2 + (-m)^2}} = \frac{1}{\sqrt{2}}$ $\frac{1}{\sqrt{m^4 + m^2}} = \frac{1}{\sqrt{2}}$ Squaring both sides: $m^4 + m^2 = 2$ $m^4 + m^2 - 2 = 0$ This is a quadratic equation in $m^2$. Let $k = m^2$. $k^2 + k - 2 = 0$ Factoring, we get $(k+2)(k-1) = 0$. So, $k = -2$ or $k = 1$. Since $k = m^2$, $m^2$ must be non-negative. Thus, $m^2 = 1$, which gives $m = \pm 1$.

The two common tangents are: For $m=1$: $y = x + 1$ (Tangent $T_1$) For $m=-1$: $y = -x - 1$ (Tangent $T_2$)

3. Find the Points of Contact on the Parabola (R and S): For a parabola $y^2 = 4ax$, the point of contact for the tangent $y = mx + \frac{a}{m}$ is $(\frac{a}{m^2}, \frac{2a}{m})$. Here $a=1$. For $m=1$: $R = (\frac{1}{1^2}, \frac{2(1)}{1}) = (1, 2)$. For $m=-1$: $S = (\frac{1}{(-1)^2}, \frac{2(1)}{-1}) = (1, -2)$.

4. Find the Points of Contact on the Circle (P and Q): For a circle $x^2 + y^2 = r^2$, the point of contact $(x_c, y_c)$ for a tangent line $y = mx + c$ can be found by using the fact that the normal to the tangent at $(x_c, y_c)$ passes through the center $(0,0)$. The slope of the normal is $\frac{y_c}{x_c}$, and it is perpendicular to the tangent, so its slope is $-\frac{1}{m}$. Thus, $\frac{y_c}{x_c} = -\frac{1}{m}$. Also, $x_c^2+y_c^2=r^2$.

For $T_1: y = x+1 \Rightarrow m=1$. $\frac{y_c}{x_c} = -\frac{1}{1} = -1 \Rightarrow y_c = -x_c$. Substitute into $x^2+y^2=\frac{1}{2}$: $x_c^2 + (-x_c)^2 = \frac{1}{2} \Rightarrow 2x_c^2 = \frac{1}{2} \Rightarrow x_c^2 = \frac{1}{4} \Rightarrow x_c = \pm \frac{1}{2}$. If $x_c = \frac{1}{2}$, then $y_c = -\frac{1}{2}$. Point $(\frac{1}{2}, -\frac{1}{2})$. Check on $y=x+1$: $-\frac{1}{2} = \frac{1}{2}+1 = \frac{3}{2}$ (False). If $x_c = -\frac{1}{2}$, then $y_c = \frac{1}{2}$. Point $(-\frac{1}{2}, \frac{1}{2})$. Check on $y=x+1$: $\frac{1}{2} = -\frac{1}{2}+1 = \frac{1}{2}$ (True). So, $P = (-\frac{1}{2}, \frac{1}{2})$.

For $T_2: y = -x-1 \Rightarrow m=-1$. $\frac{y_c}{x_c} = -\frac{1}{-1} = 1 \Rightarrow y_c = x_c$. Substitute into $x^2+y^2=\frac{1}{2}$: $x_c^2 + x_c^2 = \frac{1}{2} \Rightarrow 2x_c^2 = \frac{1}{2} \Rightarrow x_c^2 = \frac{1}{4} \Rightarrow x_c = \pm \frac{1}{2}$. If $x_c = \frac{1}{2}$, then $y_c = \frac{1}{2}$. Point $(\frac{1}{2}, \frac{1}{2})$. Check on $y=-x-1$: $\frac{1}{2} = -\frac{1}{2}-1 = -\frac{3}{2}$ (False). If $x_c = -\frac{1}{2}$, then $y_c = -\frac{1}{2}$. Point $(-\frac{1}{2}, -\frac{1}{2})$. Check on $y=-x-1$: $-\frac{1}{2} = -(-\frac{1}{2})-1 = \frac{1}{2}-1 = -\frac{1}{2}$ (True). So, $Q = (-\frac{1}{2}, -\frac{1}{2})$.

5. Calculate the Area of Quadrilateral PQRS: The vertices are $P(-\frac{1}{2}, \frac{1}{2})$, $Q(-\frac{1}{2}, -\frac{1}{2})$, $R(1, 2)$, $S(1, -2)$. Notice that points P and Q share the same x-coordinate ($x = -\frac{1}{2}$), forming a vertical line segment. Points R and S also share the same x-coordinate ($x = 1$), forming another vertical line segment. Since PQ and RS are both vertical segments, they are parallel to each other. Therefore, PQRS is a trapezium.

Length of parallel side PQ = $| \frac{1}{2} - (-\frac{1}{2}) | = |1| = 1$. Length of parallel side RS = $| 2 - (-2) | = |4| = 4$. The height $h$ of the trapezium is the perpendicular distance between the lines $x = -\frac{1}{2}$ and $x = 1$. Height $h = |1 - (-\frac{1}{2})| = |1 + \frac{1}{2}| = \frac{3}{2}$.

Area of trapezium = $\frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$ Area = $\frac{1}{2} \times (PQ + RS) \times h$ Area = $\frac{1}{2} \times (1 + 4) \times \frac{3}{2}$ Area = $\frac{1}{2} \times 5 \times \frac{3}{2}$ Area = $\frac{15}{4}$.

6. Find $\alpha + \beta$: The area is given as $\frac{\alpha}{\beta}$. So $\alpha = 15$ and $\beta = 4$. $\alpha$ and $\beta$ are coprime positive integers (15 and 4 share no common factors other than 1). We need to find $\alpha + \beta = 15 + 4 = 19$.