Solveeit Logo
Login

Question

Question: The common chord of \[{x^2} + {y^2} - 4x - 4y = 0\] and \[{x^2} + {y^2} = 16\] subtends at the origi...

The common chord of x2+y2−4x−4y=0{x^2} + {y^2} - 4x - 4y = 0 and x2+y2=16{x^2} + {y^2} = 16 subtends at the origin at an angle equal to
A. π6\dfrac{\pi }{6}
B. π4\dfrac{\pi }{4}
C. π3\dfrac{\pi }{3}
D. π2\dfrac{\pi }{2}

Explanation

Solution

Here, we will find the angle subtended at the origin. We will find the equation of the common chord by using the condition of the common chord. Thus we will find the equation of the common chord. By using the equation of the common chord we will find the angle. Thus we obtain the angle of the common chord subtended at the origin.

Formula Used
Equation of common chord is given by S1−S2=0{S_1} - {S_2} = 0

Complete Step by Step Solution:
We are given that the common chord of x2+y2−4x−4y=0{x^2} + {y^2} - 4x - 4y = 0 and x2+y2=16{x^2} + {y^2} = 16 subtends at the origin.
Let S1:x2+y2−4x−4y=0{S_1}:{x^2} + {y^2} - 4x - 4y = 0 and S2:x2+y2−16=0{S_2}:{x^2} + {y^2} - 16 = 0
The first equation is of the form of the equation of the circle whose centre is at some point but not at the origin. The second equation is of the form of the equation of the circle whose centre is at the origin.
Equation of common chord is given by S1−S2=0{S_1} - {S_2} = 0
By substituting the equation of the circle, we get
⇒S1−S2=0\Rightarrow {S_1} - {S_2} = 0
⇒x2+y2−4x−4y−x2−y2+16=0\Rightarrow {x^2} + {y^2} - 4x - 4y - {x^2} - {y^2} + 16 = 0
⇒−4x−4y+16=0\Rightarrow - 4x - 4y + 16 = 0
By changing the signs of the variables, we get
⇒4x+4y−16=0\Rightarrow 4x + 4y - 16 = 0
Dividing by 4 on both the sides, we get
⇒x+y−4=0\Rightarrow x + y - 4 = 0
By rewriting the equation, we get
⇒x+y=4\Rightarrow x + y = 4
Thus the equation of a line is equally inclined at the axes.
We will draw both the circles from the given equations of circles with a common chord at the origin.

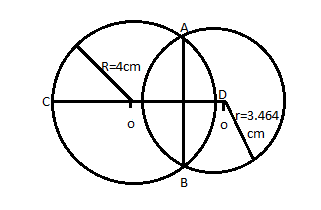
Thus the angle subtended by the common chord at origin is π2\dfrac{\pi }{2}.

Therefore, the common chord of x2+y2−4x−4y=0{x^2} + {y^2} - 4x - 4y = 0 and x2+y2=16{x^2} + {y^2} = 16 subtends at the origin at an angle equal to π2\dfrac{\pi }{2}.

Note:
We know that a chord is a straight line segment whose both the end points lie on the circle. We should know that if the chords of the curve are at right angles, then they are said to be perpendicular. Equal chords of a circle are equidistant from the radius of the circle. Equal chords of a circle subtend equal angles at the centre. Also, the common chord of two circles is also the point of intersection of two circles.