Solveeit Logo
Login

Question

Question: The combined equation of the three sides of a triangle is \[({{x}^{2}}-{{y}^{2}})(2x+3y-6)=0\]. If \...

The combined equation of the three sides of a triangle is (x2−y2)(2x+3y−6)=0({{x}^{2}}-{{y}^{2}})(2x+3y-6)=0. If (−2,a)\left( -2,a \right) is an interior point and (b,1)\left( b,1 \right) is an exterior point of the triangle then
(a) 2<a<1032 < a < \dfrac{10}{3}
(b) −2<a<103-2 < a < \dfrac{10}{3}
(c) −1<b<92-1 < b < \dfrac{9}{2}
(d) −1<b<1-1 < b < 1

Explanation

Solution

Hint: Convert the given family of lines into separate lines. Find out the inequality for point (−2,a)\left( -2,a \right) to be interior point, and then use the opposite inequality for point (b,1)\left( b,1 \right), as this is exterior point.

Complete step-by-step answer:
The combined equation of the three sides of a triangle is (x2−y2)(2x+3y−6)=0({{x}^{2}}-{{y}^{2}})(2x+3y-6)=0.
This can be written as,
(x−y)(x+y)(2x+3y−6)=0(x-y)(x+y)(2x+3y-6)=0
Therefore, the three sides of the triangle are,
x−y=0,x+y=0,2x+3y−6=0x-y=0,x+y=0,2x+3y-6=0
Plotting the equations, we get

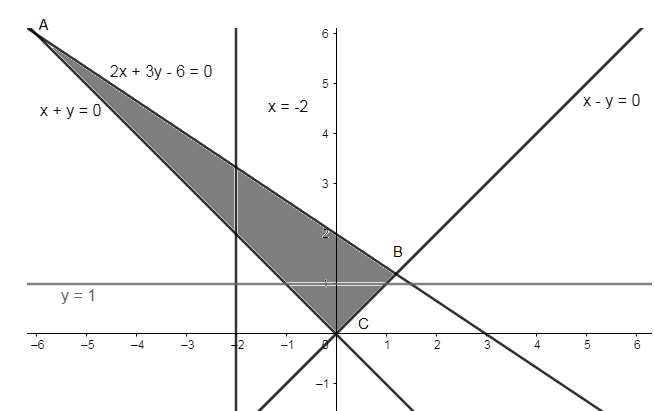
As (−2,a)\left( -2,a \right) is an interior point, so the interior point will lie on the equation x=−2x=-2.
As the equation x=−2x=-2 passes through the lines AB and AC. So, substituting the value of ‘x’ in these equations, we get
x+y=0⇒−2+y=0x+y=0\Rightarrow -2+y=0
⇒y=2\Rightarrow y=2
As here we are considering interior points, so 2Similarly,\[2x+3y−6=0⇒2(−2)+3y=62Similarly, \[2x+3y-6=0\Rightarrow 2(-2)+3y=6
⇒−4+3y=6⇒3y=6+4\Rightarrow -4+3y=6\Rightarrow 3y=6+4
⇒y=103\Rightarrow y=\dfrac{10}{3}
So, the value of ‘a’ for it to be inside the triangle will be,
2<a<1032< a <\dfrac{10}{3}

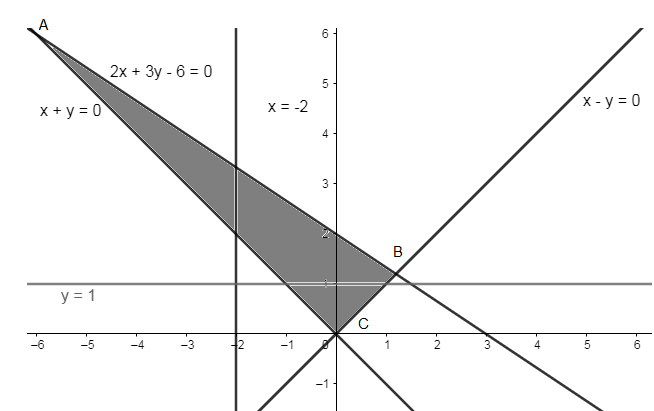
As (b,1)\left( b,1 \right) is an exterior point, so the exterior point will lie on the equation y=1y=1.
As the equation y=1y=1 passes through the lines BC and AC. So, substituting the value of ‘y’ in these equations, we get
x+y=0⇒x+1=0x+y=0\Rightarrow x+1=0
⇒x=−1\Rightarrow x=-1
As here we are considering exterior points, so −1Similarly,\[x−y=0⇒x−1=0-1Similarly, \[x-y=0\Rightarrow x-1=0
⇒x=1\Rightarrow x=1
So, the value of ‘b’ for it to be outside the triangle will be,
−1<b<1-1 < b < 1
Hence the correct options are (a) and (d).

Note: We can solve this by finding the equations of all the three sides then applying the condition for two points lying on same side, i.e., if two points A and B lie on same side of the line L, then the formula will be,LALB<0{{L}_{A}}{{L}_{B}}<0. This will be a lengthy process.