Question

The combined equation of pair of lines through the origin each of which makes an angle of $30^\circ$ with Y-axis is
A.${x^2} - {y^2} = 0$
B.$\sqrt 3 {x^2} - 4xy + \sqrt 3 {y^2} = 0$
C.$3{x^2} - {y^2} = 0$
D.${x^2} - 3{y^2} = 0$

Answer 1

Here, we will find the combined equation of the pair of lines. We will find the slope of the pair of lines and then by using the equation of the line with the slope of the pair of lines. We will combine both the equations to form the combined equation of a pair of lines through the origin.

Formula Used:
We will use the following formula:
1.Slope of the line is given by the formula $m = \tan \theta$
2.Equation of the line is of the form $y = mx + c$

Complete step-by-step answer:

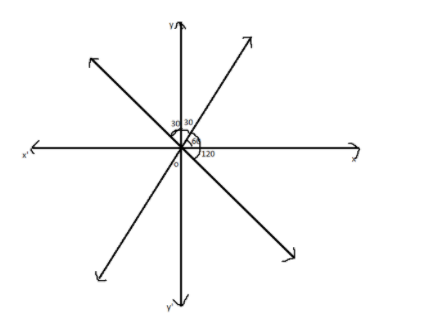
We are given the line which is at y- axis.
We will find the combined equation of lines through the origin each of which makes an angle of $30^\circ$ with Y-axis.
Now, we will find the slope of the line which is at $60^\circ$ from the line.
Slope of the line is given by the formula $m = \tan \theta$
$\Rightarrow$ Slope of the line ${m_1} = \tan 60^\circ$
$\Rightarrow$ Slope of the line ${m_1} = \sqrt 3$
Now, we will find the slope of the line which is at $120^\circ$ from the line.
Slope of the line is given by the formula $m = \tan \theta$
$\Rightarrow$ Slope of the line ${m_2} = \tan 120^\circ$
$\Rightarrow$ Slope of the line ${m_2} = - \sqrt 3$
Equation of the line is of the form $y = mx + c$
$\Rightarrow$ Equation of the first line is of the form $y = {m_1}x + c$
$\Rightarrow$ Equation of the first line is of the form $y = \sqrt 3 x$
$\Rightarrow$ Equation of the first line is of the form $y - \sqrt 3 x = 0$
Equation of the line is of the form $y = mx + c$
$\Rightarrow$ Equation of the second line is of the form $y = {m_1}x + c$
$\Rightarrow$ Equation of the second line is of the form $y = - \sqrt 3 x$
$\Rightarrow$ Equation of the second line is of the form $y + \sqrt 3 x = 0$
Now, by multiplying both the equations of line, we get
$\Rightarrow \left( {y - \sqrt 3 x} \right)\left( {y + \sqrt 3 x} \right) = 0$
Now, by using the algebraic identity, we get
$\Rightarrow {y^2} - {\left( {\sqrt 3 x} \right)^2} = 0$
$\Rightarrow {y^2} - 3{x^2} = 0$
By rewriting the equation, we get
$\Rightarrow 3{x^2} - {y^2} = 0$
Therefore, the combined equation of pair of lines through the origin each of which makes an angle of $30^\circ$ with Y-axis is $3{x^2} - {y^2} = 0$

Note: We know that the equation of line is of the form slope-intercept form, intercept form and normal form. We know that slope is defined as the ratio of change in the y axis to the change in the x axis. Slope can be represented in the parametric form and in the point form. A point crossing the x-axis is called x-intercept and A point crossing the y-axis is called the y-intercept. We are using the slope-intercept form to find the equation of line.