Question

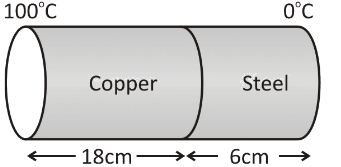
The coefficient of thermal conductivity is $9$ times that of steel. In the composite cylinder bar shown in the figure, what will be the temperature at the junction of copper and steel?

A. $75^\circ {\text{C}}$
B. $67^\circ {\text{C}}$
C. $25^\circ {\text{C}}$
D. $33^\circ {\text{C}}$

Answer 1

First of all, we will find a relation between the coefficient of thermal conductivity of copper and steel. After that we will use the expression for the rate of heat transfer. Heat transfer for both the metals will be exactly the same. We will manipulate accordingly and find the result.

Complete step by step answer:
In the given question, we are supplied the following data:
There are two metals in a composite cylinder bar which consists of copper and steel.We are also given that the coefficient of thermal conductivity is $9$ times that of steel. We are asked to find out the temperature at the junction of copper and steel.

To begin with, we have the temperature at the end of the copper metal is $100^\circ {\text{C}}$ and the temperature at the end of the steel metal is $0^\circ {\text{C}}$ . The length of the copper metal is $18\,{\text{cm}}$ while the length of the steel metal is $6\,{\text{cm}}$ .

Let the coefficient of thermal conductivity for steel metal be $k$ and the coefficient of thermal conductivity for copper metal will be $9k$ .Again, the temperature at the junction of copper and steel will be $T$ .Both the metals are in a series combination. Again, the rate of heat transfer will be equal. The rate of heat transfer for the metal can be written as:
$\dfrac{{\Delta Q}}{{\Delta t}} = \dfrac{{k \times A \times \Delta T}}{l}$ …… (1)
Where,
$\Delta Q$ indicates the transferred heat energy.
$\Delta t$ indicates the time duration.
$k$ indicates the coefficient of thermal conductivity.
$A$ indicates the area of the cross section.
$\Delta T$ indicates the temperature difference.
$l$ indicates the length of the conductor.

Now, we can equate the rate of heat transfer for the copper and steel, as given below:
${\left( {\dfrac{{\Delta Q}}{{\Delta t}}} \right)_{{\text{Copper}}}} = {\left( {\dfrac{{\Delta Q}}{{\Delta t}}} \right)_{{\text{Steel}}}} \\\ \Rightarrow \dfrac{{9k \times A \times \left( {100 - T} \right)}}{{18}} = \dfrac{{k \times A \times \left( {T - 0} \right)}}{6} \\\ \Rightarrow \dfrac{{9 \times \left( {100 - T} \right)}}{3} = T \\\ \Rightarrow 300 - 3T = T \\\ \Rightarrow 300 = 4T \\\ \Rightarrow T = \dfrac{{300}}{4} \\\ \therefore T = 75^\circ {\text{C}}$
Hence, the temperature at the junction will be $75^\circ {\text{C}}$ .

The correct option will be A.

Note: While solving the problem it is important to note that the area of the cross section of the two metal bars will be exactly equal as they are the part of the same cylindrical bar. We can also find the same solution by doing in some alternative way, which uses the formula as given below:
$T = \dfrac{{\dfrac{{{k_1}}}{{{l_1}}} \times {T_1} + \dfrac{{{k_2}}}{{{l_2}}} \times {T_2}}}{{\dfrac{{{k_1}}}{{{l_1}}} + \dfrac{{{k_2}}}{{{l_2}}}}}$
Where $T$ indicates the final junction temperature.