Question
Question: The co-ordinates of image of point object P formed after two successive reflection in situation as s...
The co-ordinates of image of point object P formed after two successive reflection in situation as shown in figure considering first reflection at concave mirror and then at convex.
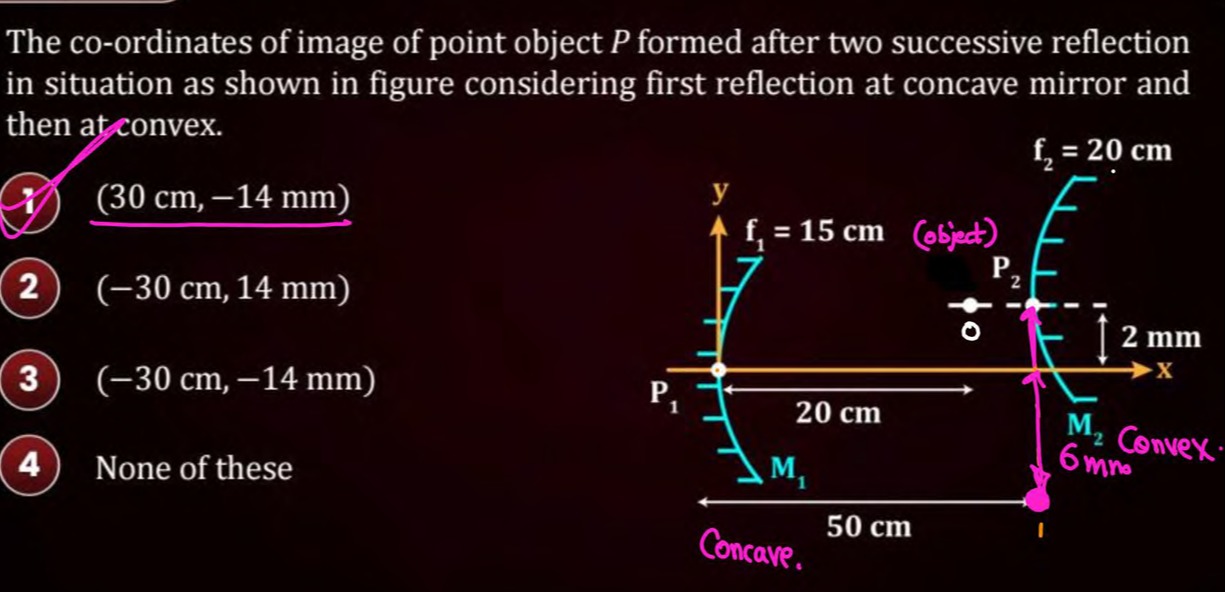
30 cm, -14 mm
-30 cm, 14 mm
-30 cm, -14 mm
None of these
None of these
Solution
Let the object be at x=−20 cm, y=6 mm. For the concave mirror (f1=−15 cm): Using the mirror formula v11−u11=f11, we have v11−−201=−151. v11=−151−201=60−4−3=−607. v1=−760 cm. Magnification m1=−u1v1=−−20−60/7=−73. Image height hi1=m1ho=−73×6=−718 mm. The first image is at (−760 cm,−718 mm).
For the convex mirror (f2=20 cm), the pole is at x=50 cm. The object distance u2=50−(−760)=50+760=7350+60=7410 cm. Since the object is to the left of the mirror, u2=−7410 cm. The object height for the convex mirror is ho2=−718 mm. Using the mirror formula v21−u21=f21: v21−−410/71=201 v21+4107=201 v21=201−4107=41041−14=41027. v2=27410 cm. The x-coordinate of the final image is xfinal=50+v2=50+27410=271350+410=271760≈65.185 cm. Magnification m2=−u2v2=−−410/7410/27=277. The height of the final image is hi2=m2ho2=277×(−718)=−2718=−32 mm. The calculated coordinates (271760 cm,−32 mm) do not match any of the given options. Therefore, "None of these" is the correct answer.
