Question

The circumcenter of the triangle with vertices $(0,30)$ , $(4,0)$ and $(30,0)$ is
A.$(10,10)$
B.$(10,12)$
C.$(12,12)$
D.$(15,15)$
E.$(17,17)$

Answer 1

Hint : The circumcenter is the center point of the circumcircle drawn around a polygon. The circumcircle of a polygon is the circle that passes through all of its vertices and the center of that circle is called the circumcenter. All polygons that have a circumcircle are known as cyclic polygons. Only regular polygons, triangles, rectangles, and right-kites can have the circumcircle and thus the circumcenter.

Complete step-by-step answer :
Steps to construct the circumcenter of a triangle:
Step 1: Draw the perpendicular bisectors of all the sides of the triangle using a compass.
Step 2: Extend all the perpendicular bisectors to meet at a point. Mark the intersection point as O, this is the circumcenter.
Step 3: Using a compass and keeping O as the center and any vertex of the triangle as a point
on the circumference, draw a circle, this circle is our circumcircle whose center is O.

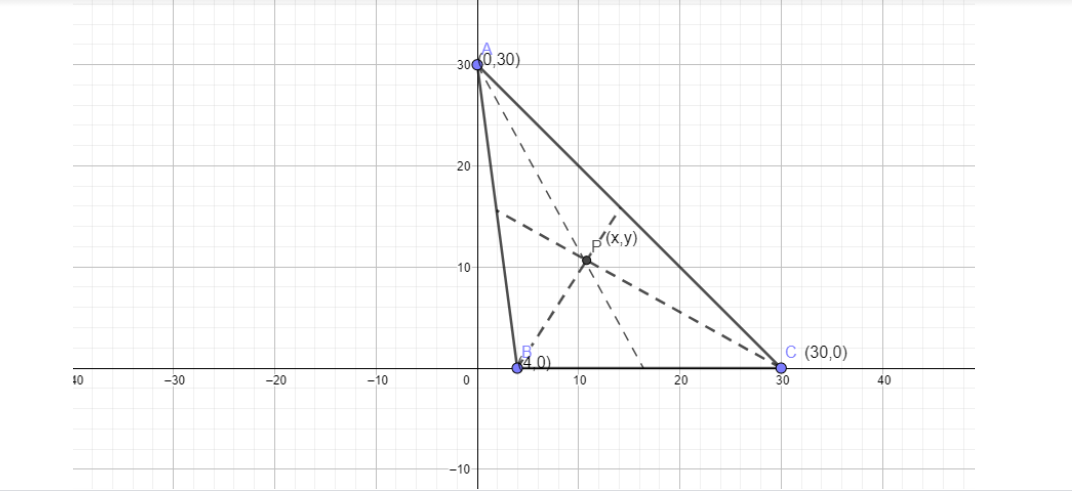
Assume that the circumcenter of a triangle is P(x,y)
The vertices are given to us as follows
A $(0,30)$
B $(4,0)$
C $(30,0)$
we have the following equations using the distance formula :
$AP = \sqrt {{{(x - 0)}^2} + {{\left( {y - 30} \right)}^2}}$
$BP = \sqrt {{{(x - 4)}^2} + {{\left( {y - 0} \right)}^2}}$
And
$CP = \sqrt {{{(x - 30)}^2} + {{\left( {y - 0} \right)}^2}}$
Since the vertices of the triangle are equidistant from the circumcenter .
Therefore we get
AP=BP=CP
Now using the first and second equality we have
$\sqrt {{{(x - 0)}^2} + {{\left( {y - 30} \right)}^2}}$ = $\sqrt {{{(x - 4)}^2} + {{\left( {y - 0} \right)}^2}}$
Squaring both the sides we get
${(x - 0)^2} + {\left( {y - 30} \right)^2}$ = ${(x - 4)^2} + {\left( {y - 0} \right)^2}$
Which simplifies to
${x^2} + {y^2} + 900 - 60y = {x^2} + 16 - 8x + {y^2}$
On further simplification we get
$900 + 60y = 16 + 8x$
On further simplification we get
$221 = 15y - 2x$ …(1)
Now using the second and third equality we get
$\sqrt {{{(x - 4)}^2} + {{\left( {y - 0} \right)}^2}} = \sqrt {{{(x - 30)}^2} + {{\left( {y - 0} \right)}^2}}$
Squaring both the sides we get
${(x - 4)^2} + {\left( {y - 0} \right)^2} = {(x - 30)^2} + {\left( {y - 0} \right)^2}$
Which simplifies to
${x^2} + 16 - 8x + {y^2} = {x^2} + 900 - 60x + {y^2}$
On further simplification we get
$884 = 52x$
Therefore we get
$x = 17$
Now putting this value of $x$ in (1) we get
$y = 17$
Therefore the point of circumcentre $(17,17)$
Therefore option (E) is the correct answer.
So, the correct answer is “Option E”.

Note : Properties of circumcenter are: Consider any triangle ABC with circumcenter O.
A) All the vertices of the triangle are equidistant from the circumcenter.
B) All the new triangles formed by joining O to the vertices are Isosceles triangles.