Solveeit Logo
Login

Question

Question: The circum radius of the triangle formed by the points (2,-1,1), (1,-3,-5) and (3,-4,-4) is: A. \(...

The circum radius of the triangle formed by the points (2,-1,1), (1,-3,-5) and (3,-4,-4) is:
A. 62\dfrac{\sqrt{6}}{2}
B.352\dfrac{\sqrt{35}}{2}
C. 412\dfrac{\sqrt{41}}{2}
D. 41\sqrt{41}A.

Explanation

Solution

Apply the distance formula, the distance formula is that in which we can find the distance between two points. It is represented by d,
d = (x2−x1)2+(y2−y1)2\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}
where are two points

Complete step by step answer:
Let A, B, C be three points: (2,-1,1), (1,-3,-5) and (3,-4,-4) respectively. Consider the two points A and B, where A is (2,-1,1) and B is (1,-3,-5) respectively.

Apply distance formula in AB:
(AB)d=(x2−x1)2+(y2−y1)2+(z2−z1)2(AB)d=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}+{{({{z}_{2}}-{{z}_{1}})}^{2}}}
Substituting the values of AB, () and () i.e (2,-1,1) and (1,-3,-5) respectively in above equation, we get:
(AB)=(1−2)2+[−3−(−1)]2+(−5−1)2(AB) = \sqrt{{{(1-2)}^{2}}+{{[-3-(-1)]}^{2}}+{{(-5-1)}^{2}}}
⇒(AB)=1+4+36\Rightarrow(AB) = \sqrt{1+4+36}
⇒(AB)=41\Rightarrow(AB) =\sqrt{41}
Consider other points BC, where B is (1,-3,-5) and C is (3,-4,-4). Let B be () and C be () respectively. Apply distance formula in BC:
(BC)=(x2−x1)2+(y2−y1)2+(z2−z1)2(BC) = \sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}+{{({{z}_{2}}-{{z}_{1}})}^{2}}}
Substituting the values of BC, () and () i.e (1,-3,-5) and (3,-4,-4) respectively in above equation, we get:
(BC)=(3−1)2+(−4−(−3))2+(−4−(−5))2(BC) =\sqrt{{{(3-1)}^{2}}+{{(-4-(-3))}^{2}}+{{(-4-(-5))}^{2}}}
⇒(BC)=(2)2+(−1)2+(1)2\Rightarrow(BC) = \sqrt{{{(2)}^{2}}+{{(-1)}^{2}}+{{(1)}^{2}}}
⇒(BC)=6\Rightarrow (BC) = \sqrt{6}

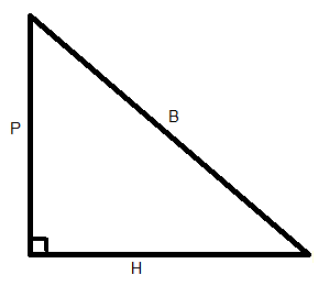
i.e:H2=P2+B2{{H}^{2}}={{P}^{2}}+{{B}^{2}}
Consider a right angle triangle haven point A, B, C. According to the Pythagoras theorem:
H2=P2+B2{{H}^{2}}={{P}^{2}}+{{B}^{2}}
In the given triangle ABC, where C is the right angle that make 90degree angle, so it becomes: AB2=AC2+BC2A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}} ………………….Equ(a)
where AB is the hypotenuse of the triangle, AC is the perpendicular of the triangle and BC is the base of the triangle. According to the given question, substituting the value of AB, AC and BC in the equation (A), we get:
AB2=AC2+BC2A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}
L.H.S: AB2=[41]2A{{B}^{2}}={{\left[ \sqrt{41} \right]}^{2}}
R.H.S: AC2+BC2=[35]2+[6]2A{{C}^{2}}+B{{C}^{2}}={{\left[ \sqrt{35} \right]}^{2}}+{{\left[ \sqrt{6} \right]}^{2}}
AC2+BC2=41A{{C}^{2}}+B{{C}^{2}} =41
So,
AB2=AC2+BC2A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}
The triangle ABC is a right angle triangle.Now the circum radius of the right angle triangle is equal to the half of the hypotenuse.
So,circumradius = 412\dfrac{\sqrt{41}}{2}
The circum radius of the given equation is 412\dfrac{\sqrt{41}}{2}.In the figure given below, you can see how the circumradius of the right angled triangle is equal to half of its hypotenuse.

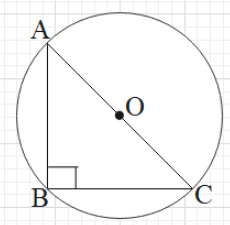
Hence, option C is correct.

Note: In the given question, the distance formula is applied between two points. Distance formula is an application of the Pythagoras theorem. By using the Pythagoras theorem the result is produced.Circumradius is the radius of a circle which circumscribes the given triangle. Distances of all vertices from circumcentre are equal and are called circumradius.