Question

The circum radius of the triangle formed by the points $\left( 1,2,-3 \right),\left( 2,-3,1 \right)$ and$\left( -3,1,2 \right)$ is: A.$\sqrt{14}$$$$$ B.14
C.$\sqrt{13}$$$$$
D.0$$$$

Answer 1

We find the lengths of the sides using the distance formula between any two points with coordinates $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right),\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$in space as $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}$. We apply formula on vertices and find that the lengths of the sides are equal. We use the formula for circumradius $r$ of an equilateral triangle $r=\dfrac{a}{\sqrt{3}}$ where $a$ is the lengths of sides to get the required result.$$$$

Complete step by step answer:
We know that the distance $d$ between two points with coordinates $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right),\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ in the three dimensional space is given by
$d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}$
We also the circumcircle of a triangle is a circle that passes through the vertices of the circles. The centre of the circumcircle is called circumcentre and the radius of the circum circle is called circumradius. The length of the circumradius with length of the circle is given by
$r=\dfrac{abc}{\sqrt{\left( a+b+c \right)\left( -a+b+c \right)\left( a-b+c \right)\left( a+b-c \right)}}$
If the triangle is equilateral triangle $a=b=c$ the formula for circum radius reduces to,
$r=\dfrac{a}{\sqrt{3}}$
We are given the coordinates of the vertices of the triangle $\left( 1,2,-3 \right),\left( 2,-3,1 \right)$ and $\left( -3,1,2 \right)$. We are asked to find the length of the circumradius. We denote the vertices as $A\left( 1,2,-3 \right),B\left( 2,-3,1 \right)$ and$C\left( -3,1,2 \right)$. We draw the rough figure with circumcentre O below,$$$$

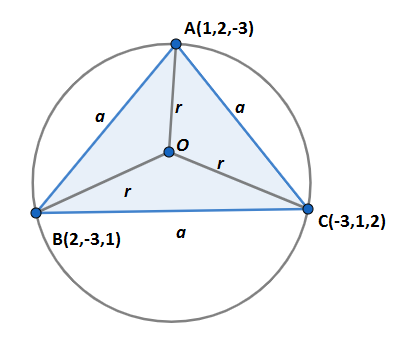
So we first find lengths of the sides using the distance formula. We find AB whose endpoints are $A\left( 1,2,-3 \right),B\left( 2,-3,1 \right)$. So we have
$AB=\sqrt{{{\left( 2-1 \right)}^{2}}+{{\left( -3-2 \right)}^{2}}+{{\left( 1-\left( -3 \right) \right)}^{2}}}=\sqrt{1+25+16}=\sqrt{42}$
We find AC whose endpoints are $A\left( 1,2,-3 \right),C\left( -3,1,2 \right)$. So we have,
$AC=\sqrt{{{\left( -3-1 \right)}^{2}}+{{\left( 1-2 \right)}^{2}}+{{\left( 2-\left( -3 \right) \right)}^{2}}}=\sqrt{16+1+25}=\sqrt{42}$
We find BC whose endpoints are $B\left( 2,-3,1 \right),C\left( -3,1,2 \right)$
$BC=\sqrt{{{\left( -3-2 \right)}^{2}}+{{\left( 1-\left( -3 \right) \right)}^{2}}+{{\left( 2-1 \right)}^{2}}}=\sqrt{25+16+1}=\sqrt{42}$
We see that $AB=BC=AC$. So the given triangle is an equilateral triangle. We use the formula for length of circumradius of equilateral triangle with side $a$ as and have the radius as
$r=\dfrac{a}{\sqrt{3}}=\dfrac{\sqrt{42}}{\sqrt{3}}=\sqrt{\dfrac{42}{3}}=\sqrt{14}$

So, the correct answer is “Option A”.

Note: We note that distance is always a positive quantity and hence we have rejected negative square roots. We can alternatively solve by finding the circumcentre O and distance between O to any vertex. We find the circumcenter as a point of intersection lines that passes through midpoints of sides and lying in the plane of the triangle. The circumcentre is given by $\left( \dfrac{p{{x}_{1}}+q{{y}_{1}}+r{{z}_{1}}}{p+q+r},\dfrac{p{{x}_{2}}+q{{y}_{2}}+r{{z}_{2}}}{p+q+r},\dfrac{p{{x}_{3}}+q{{y}_{3}}+r{{z}_{3}}}{p+q+r} \right)$ where $p={{a}^{2}}\left( {{b}^{2}}+{{c}^{2}}-{{a}^{2}} \right),q={{b}^{2}}\left( {{c}^{2}}+{{a}^{2}}-{{b}^{2}} \right),r={{c}^{2}}\left( {{a}^{2}}+{{b}^{2}}-{{c}^{2}} \right)$ are called barycentric coordinates.