Question
Question: The circuit shown in the figure contains two diodes each with a forward resistance of \(50\Omega \) ...
The circuit shown in the figure contains two diodes each with a forward resistance of 50Ω and the infinite backward resistance. If the battery voltage is 6V , the current through the 100Ω resistance ( in amperes ) is
(A) zero
(B) 0.02
(C) 0.03
(D) 0.036
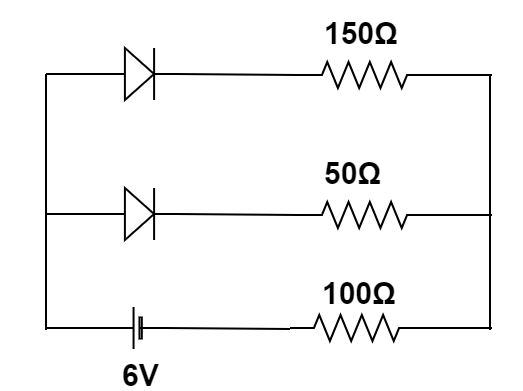
Solution
Knowledge of forward and reverse bias conditions for a PN junction diode is required. Given, the resistance of the diode will be 50Ω in forward biasing condition and infinity in reverse biasing condition. Additionally, ohm’s law would also be required to find the current value.
Formula used:
V=IR
⇒I=RV
Complete Step-by-step solution: Let’s remake the circuit, by putting in the signs of the potential of the battery connected, the currents flowing through different arms of the circuit.
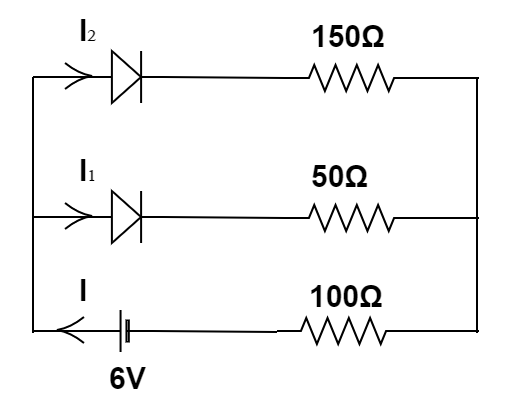
To understand the division of the current flowing through the circuit, we will use Kirchhoff's current law. Hence, considering the amount of current to be flowing through the resistance 100Ω to be I . Then, the circuit breaks into two arms. Hence, the current also gets divided into I1 and I2 .
Hence, the sum of I1 and I2 will be I .
We will now discuss the diodes. A PN junction diode is a semiconductor containing excess electrons and holes on each end of the diode and a PN junction interface in between. A common region is formed between the P and the N side having equal amounts of holes and electrons.
In this case, both the diodes are in forward biased condition. Hence the resistance offered by the diode in a forward bias condition is 50Ω .
Taking this into account,
The circuit can be simplified into this form
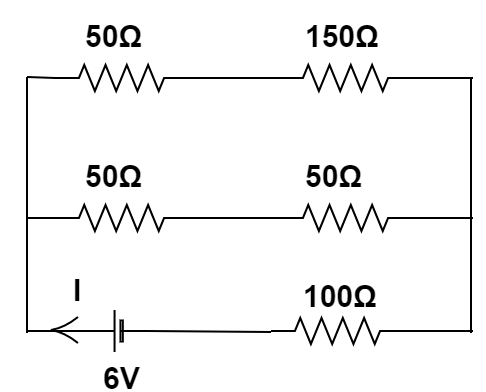
Therefore, we have to find the equivalent resistance of this circuit,
As 50Ω resistor and 150Ω resistor are in series. Therefore, the overall resistance of this arm is 200Ω . Similarly, the overall resistance of the other arm is 100Ω .
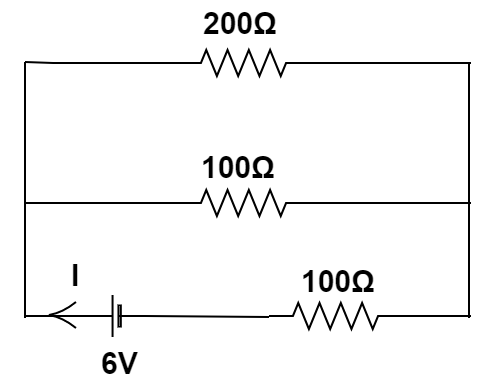
Since 200Ω resistor and 100Ω resistor are in parallel combination,
Req=200+100200×100
⇒Req=300200×100=3200
Hence, the circuit can be simplified as;
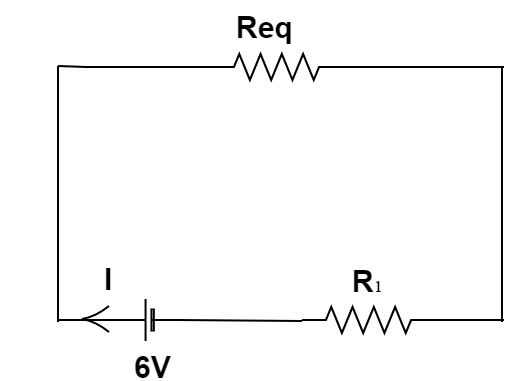
Therefore, the value of current flowing in the circuit can be found using ohm’s law:
V=IR⇒6V=IRnet
⇒6V=I(Req+R1)
On Substituting the value of Req and R1 in the above equation,
⇒6V=I(3200+100)
⇒6V=I(3500)
Solve the above equation to determine the value of I ,
⇒I=5006×3=2509
⇒I=0.036A
As a result, the amount of current flowing through the resistor 100Ω is 0.036A .
Hence, the correct option is (D).
Note: we consider the value of the net resistance in the above condition to be: Rnet=Req+R1 because the resistances are in series to each other. The net resistance of the circuit, when the resistances are connected in series is given by the sum of the resistance values of the resistors connected.
