Question

The circuit is shown.

What is current through $3\Omega$ resistance $?$

Answer 1

In this problem, first we need to find the equivalent resistance to find the value of current flowing through the resistor of resistance $3\Omega$ . In series combination the current remains the same and voltage will be different whereas in parallel combination the current will be different and voltage will be the same we use this concept to solve the problem.

Formula used:
$\to$ For series combination, the equivalent resistance is given by
${R_s} = {R_1} + {R_2} + ...... + {R_n}$
$\to$ For parallel combination, the equivalent resistance is given by
$\dfrac{1}{{{R_p}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ....... + \dfrac{1}{{{R_n}}}$
According to ohm’s law,
$V = IR$
$\Rightarrow I = \dfrac{V}{R}$

Complete step by step answer:
Step $1$ :-

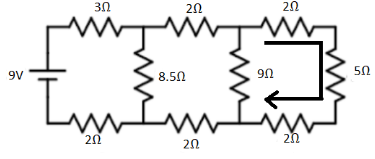
In above circuit $2\Omega$ , $5\Omega$ and $2\Omega$ are connected in series because the current is the same in these resistors as shown in above circuit. Therefore,
${R_{s1}} = {R_1} + {R_2} + {R_3}$
$\Rightarrow {R_{s1}} = 2 + 5 + 2$
$\Rightarrow {R_{s1}} = 9\Omega$ ………. $\left( 1 \right)$
Step $2$ :-

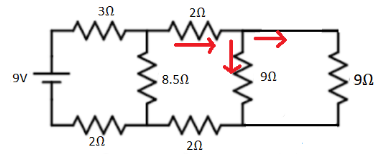
In the above circuit $9\Omega$ and $9\Omega$ are connected in parallel because the current is different in these resistors as shown in the above circuit. Therefore,
$\dfrac{1}{{{R_p}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
On substituting we get
$\dfrac{1}{{{R_{p1}}}} = \dfrac{1}{9} + \dfrac{1}{9}$
On simplifying we get
$\dfrac{1}{{{R_{p1}}}} = \dfrac{2}{9}$
Therefore, ${R_{p1}} = 4.5\Omega$ ………..$\left( 2 \right)$

Step $3$ :-

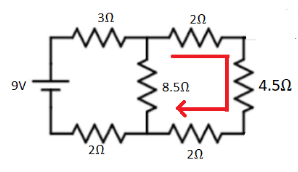
In above circuit $2\Omega$, $4.5\Omega$ and $2\Omega$ are connected in series because the current is the same in these resistors as shown in above circuit.Therefore,
${R_{s2}} = {R_1} + {R_2} + {R_3}$
$\Rightarrow {R_{s2}} = 2 + 4.5 + 2$
$\Rightarrow {R_{s2}} = 8.5\Omega$ ………. $\left( 3 \right)$

Step $4$ :-

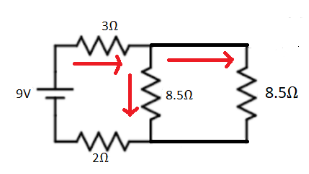
In the above circuit $8.5\Omega$ and $8.5\Omega$ are connected in parallel because the current is different in these resistors as shown in the above circuit. Therefore,
$\dfrac{1}{{{R_p}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
On substituting we get
$\dfrac{1}{{{R_{p2}}}} = \dfrac{1}{{8.5}} + \dfrac{1}{{8.5}}$
On simplifying we get
$\dfrac{1}{{{R_{p2}}}} = \dfrac{2}{{8.5}}$
Therefore, ${R_{p2}} = 4.25\Omega$ ………..$\left( 4 \right)$

Step $5$ :-

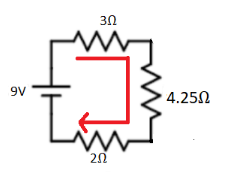
In above circuit $3\Omega$ , $4.25\Omega$ and $2\Omega$ are connected in series because the current is the same in these resistors as shown in above circuit.Therefore,
${R_{eq}} = {R_1} + {R_2} + {R_3}$
$\Rightarrow {R_{eq}} = 3 + 4.25 + 2$
$\Rightarrow {R_{eq}} = 9.25\Omega$ ………. $\left( 5 \right)$
Step $6$ :-
According to ohm’s law
$V = IR$
$\Rightarrow I = \dfrac{V}{R}$
Substituting the value of $V$ and $R$
Therefore, $I = \dfrac{9}{{9.25}}$
$\therefore I = 0.973A$

Hence current flow through $3\Omega$ resistor is $0.973A$.

Note: In an electric circuit, various components can be connected either in series or in parallel manner to produce different resistive networks. Sometimes, in the same circuit, resistors can be connected in parallel and series, across different loops to produce a more complex resistive network. Resistors are said to be in series if they are joined end to end such that the same current flows through all of them.