Question

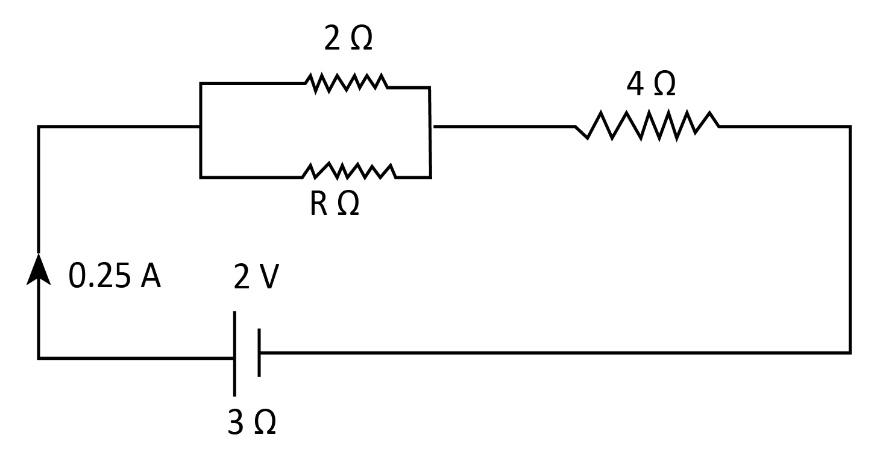
The circuit diagram in Fig. 8.53 shows three resistors $2\;\Omega$, $4\;\Omega$ and $R\;\Omega$ connected to a battery of e.m.f. $2\;{\rm{V}}$ and internal resistance $3\;\Omega$. If main current of $0.25\;{\rm{A}}$ flows through the circuit, find:
(a) the p.d. across the $4\;\Omega$ resistor,
(b) the p.d. across the internal resistance of the cell
(c) the p.d. across the $R\;\Omega$ or $2\;\Omega$ resistor, and
(d) the value of $R$.

Answer 1

In this question, we will use Ohm’s law equation for finding voltage, current or resistance. We will also identify the resistances connected in series and in parallel to find the values of electric quantities.

Complete step by step answer:
Given,
Emf of the battery, $E = 2\;{\rm{V}}$
Internal resistance of the battery, $r = 3\;\Omega$
Main current flowing through the circuit, $I = 0.25\;{\rm{A}}$
Also, let ${R_1} = 2\;\Omega$, ${R_2} = 4\;\Omega$ and ${R_3} = R\;\Omega$.

(a) The p.d. across the resistance ${R_2} = 4\;\Omega$ can be written as
${V_2} = I{R_2}$

Here ${V_2}$ is the p.d. across ${R_2}$.

Now we substitute the values $0.25\;{\rm{A}}$ for $I$ and $4\;\Omega$ for ${R_2}$ in the equation to get,

$\begin{array}{c} {V_2} = 0.25\; \times 4\;\\\ = 1\;{\rm{V}} \end{array}$

Hence, the p.d. across the resistance ${R_2}$ is $1\;{\rm{V}}$.

(b) The p.d. across the internal resistance $r$ of the cell can be written as

$V = Ir$

Now we substitute the values $0.25\;{\rm{A}}$ for $I$ and $3\;\Omega$ for $r$ in the equation to get,

$\begin{array}{c} V = 0.25\; \times 3\;\\\ = 0.75\;{\rm{V}} \end{array}$

Hence, the p.d. across the internal resistance of the cell is $0.75\;{\rm{V}}$.

(c) From the circuit diagram, we can see that the resistances ${R_1} = 2\;\Omega$ and ${R_3} = R\;\Omega$ are connected in parallel. Also, we can see that the resistance ${R_2} = 4\;\Omega$ is in series with the parallel combination of resistances ${R_1}$ and ${R_3}$.

Now we have to find the equivalent resistance of the resistances ${R_1}$ and ${R_3}$. The equivalent resistance is written as

${R_p} = \dfrac{{{R_1}{R_3}}}{{{R_1} + {R_3}}}$

Since the internal resistance of the cell $r$ and the resistance ${R_2}$ is in series with the parallel combination of resistances ${R_1}$ and ${R_3}$, we can write the equivalent resistance of the circuit as

$\begin{array}{c} {R_{eq}} = r + {R_2} + {R_p}\\\ = r + {R_2} + \dfrac{{{R_1}{R_3}}}{{{R_1} + {R_3}}} \end{array}$

Substituting the values of $r$, ${R_1}$, ${R_2}$ and ${R_3}$ in the above equation, we get

$\begin{array}{c} {R_{eq}} = 3 + 4 + \dfrac{{2 \times R}}{{2 + R}}\\\ = 7 + \dfrac{{2R}}{{2 + R}}\\\ = \dfrac{{14 + 7R + 2R}}{{2 + R}}\\\ = \dfrac{{14 + 9R}}{{2 + R}} \end{array}$

Now, the emf of the battery can be written as

$E = I{R_{eq}}$

Now we substitute $2\,{\rm{V}}$ for $E$, $0.25\;{\rm{A}}$ for $I$ and $\dfrac{{14 + 9R}}{{2 + R}}$ for ${R_{eq}}$ to get,

$2 = 0.25 \times \left( {\dfrac{{14 + 9R}}{{2 + R}}} \right)\\\ \implies 2 = \dfrac{1}{4}\left( {\dfrac{{14 + 9R}}{{2 + R}}} \right)\\\ \implies 2 = \dfrac{{14 + 9R}}{{8 + 4R}}\\\ \implies 2\left( {8 + 4R} \right) = 14 + 9R$

Simplifying further

$\begin{array}{c} 16 + 8R = 14 + 9R\\\ R = 2\;\Omega \end{array}$

So, we obtained the value of $R$ as $2\;\Omega$.

Now, the p.d. across ${R_1} = 2\;\Omega$ or ${R_3} = R\;\Omega$ can be written as

${V_1} = I{R_p}$

Now, using the equation ${R_p} = \dfrac{{{R_1}{R_3}}}{{{R_1} + {R_3}}}$ we can write

${V_1} = I\left( {\dfrac{{{R_1}{R_3}}}{{{R_1} + {R_3}}}} \right)$

Now, we substitute the values for $I$, ${R_1}$ and ${R_3}$ in the above equation to get

$\begin{array}{c} {V_1} = 0.25 \times \left( {\dfrac{{2 \times 2}}{{2 + 2}}} \right)\\\ = 0.25\,{\rm{V}} \end{array}$

Hence, the p.d. across the $R\;\Omega$ or $2\;\Omega$ resistor is $0.25\,{\rm{V}}$.m (d) From subpart (c), the value of $R$ is $2\;\Omega$..

Note:
We should note that the voltage across the resistances connected in series are different, while the current flowing through each of them will be the same. For resistances connected in parallel, the voltage across each of them will be the same, while the current is different.