Question
Question: The circles \({{x}^{2}}+{{y}^{2}}\)=4 and \({{x}^{2}}+{{y}^{2}}-4\lambda x+9=0\) have exactly two co...
The circles x2+y2=4 and x2+y2−4λx+9=0 have exactly two common tangents if λ equals
(a) 8
(b) 2
(c) 12
(d) -112
Solution
Hint: For two circles to have exactly two common tangents, they should intersect each other at two points. Use the fact that two circles intersect each other at two points of the distance between their centres is less than the sum of the radii of the two circles and greater than the difference of the radii of the two circles, i.e. ∣r1−r2∣<C1C2<r1+r2. Use the fact that the radius of a circle x2+y2+2gx+2fy+c=0 is given by r=g2+f2−c. Hence form an inequation in λ. Hence find which of the options is correct
Complete step-by-step solution -
We know that the radius of the circle x2+y2+2gx+2fy+c=0 is given by r=g2+f2−c and the centre is given by C≡(−g,−f)
Consider the circle S1:x2+y2=4
Here g = f = 0, c= -4
Hence the centre of the circle S1 is given by C1≡(0,0)
The radius of the circle S1 is given by r1=g2+f2−c=02+02−(−4)=2
Consider the circle x2+y2−4λx+9=0
Here g=−2λ,f=0,c=9
Hence the centre of the circle S2 is given by C2≡(2λ,0)
The radius of the circle S2 is given by r2=g2+f2−c=4λ2−9
The radius of the circle should be real.
Hence, we have
4λ2−9>0⇒λ2−49>0⇒(λ−23)(λ+23)>0⇒λ∈(−∞,2−3)⋃(23,∞) (i)
Now since the circles have only two common tangents, they must intersect at two points.
Hence, we have
∣r1−r2∣<C1C2<r1+r2
Now, we have
C1C2=(2λ−0)2+(0−0)2=2∣λ∣
From the inequation ∣r1−r2∣<C1C2, we have
4λ2−9−2<2∣λ∣
Since both LHS and RHS are non-negative, squaring will not change the sense of the inequality sign.
Squaring both sides, we get
4λ2−9+4−44λ2−9<4λ2⇒−44λ2−9−5<0⇒44λ2−9>−5
This inequality is true for all possible values of λ since the square root of a term is non-negative.
From the inequation C1C2<∣r1+r2∣, we have
2∣λ∣<4λ2−9+2
Since both LHS and RHS are non-negative, squaring will not change the sense of the inequality sign.
Squaring both sides, we get
4λ2<4λ2−9+4+44λ2−9⇒44λ2−9>5
Squaring both sides again, we get
16(4λ2−9)>25⇒4λ2−9>1625⇒4λ2>1625+144=16169⇒λ2>64169⇒(λ−813)(λ+813)>0⇒λ∈(−∞,8−13)⋃(813,∞) (ii)
From (i) and (ii), we have
λ∈(−∞,8−13)⋃(813,∞)
Clearly all of the options [p],[q],[r] and [s] are in this range.
Note: To ease your understanding, here’s a plot on the number line of the possible values of λ that we found out :
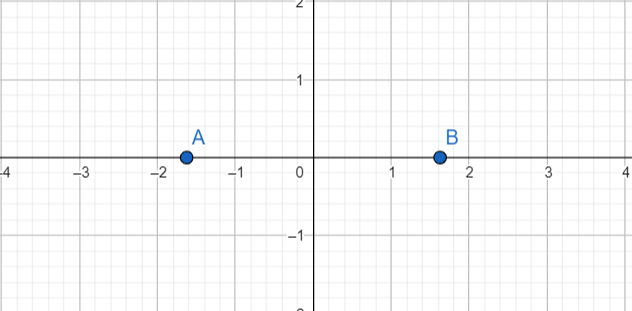
Here, A and B represent −813 and +813 respectively. The values of λ lie on the side where the absolute of the values are >+813 .
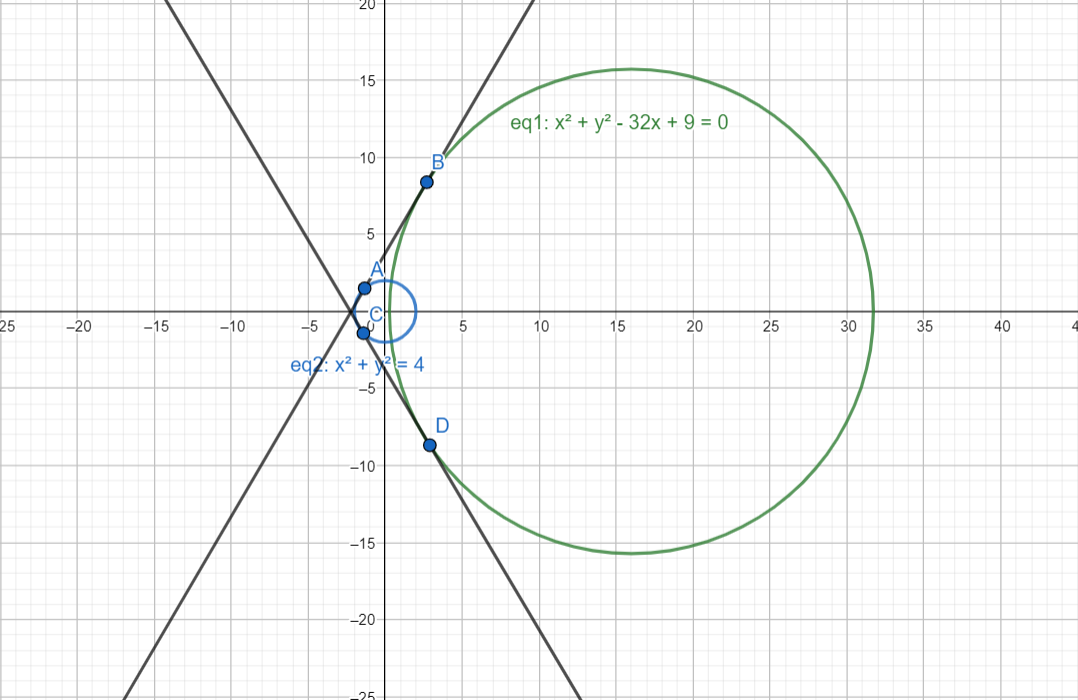
Here are the circles and their tangents with each value of λ as given in the options :
When λ = 8 :
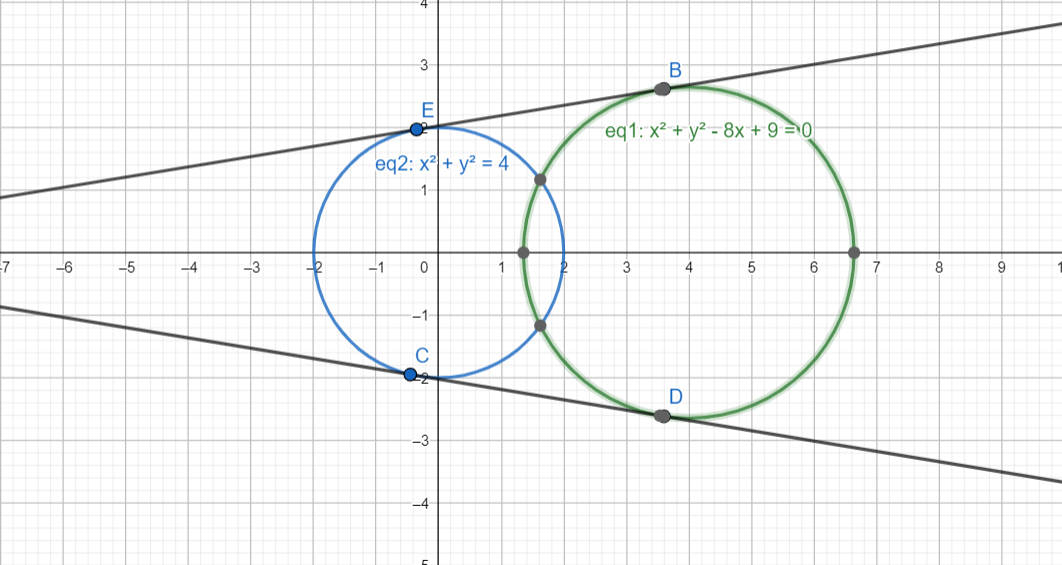
When λ = 2:
When λ = 12 :
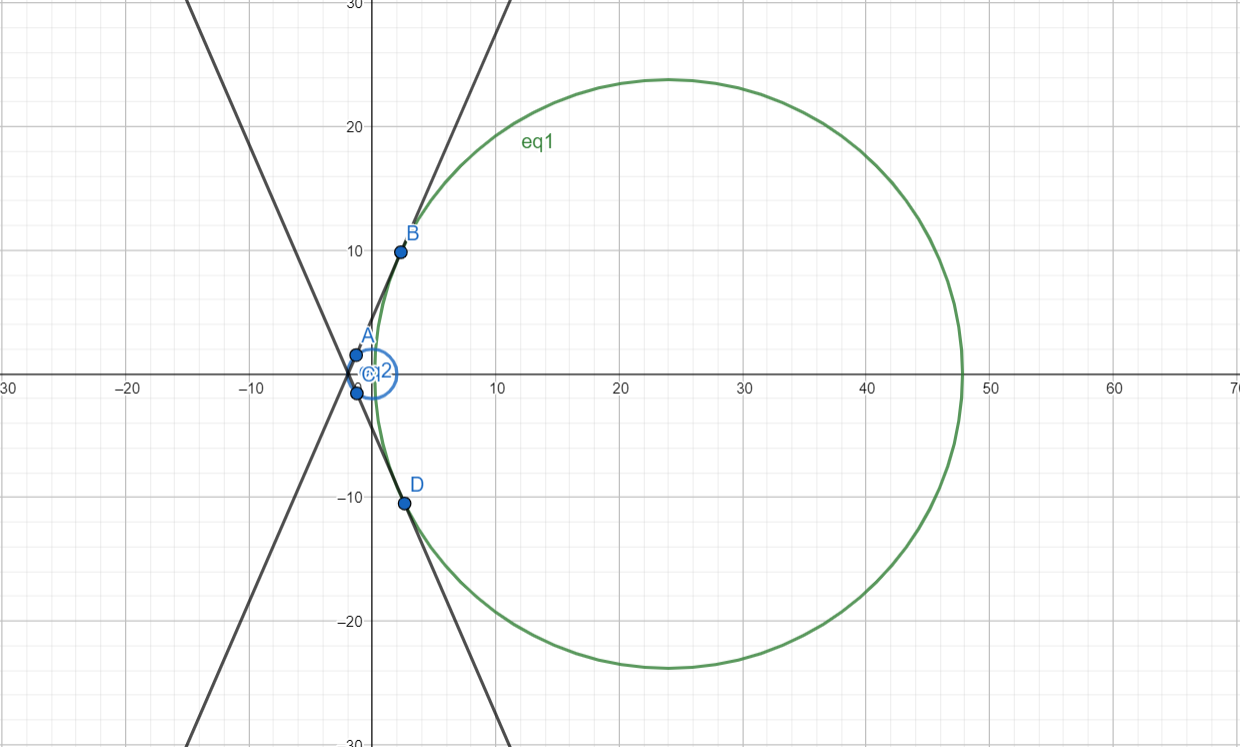
When λ = -112 :