Question

The circles ${{x}^{2}}+{{y}^{2}}+2ax+c=0$ and ${{x}^{2}}+{{y}^{2}}+2bx+c=0$have no common tangents if

& 1)ab>0,c<0 \\\ & 2)ab<0,c>0 \\\ & 3)ab>0,c>0 \\\ & 4)ab>0,c<0 \\\ & \\\ \end{aligned}$$

Answer 1

The two equations given in the question represent two different circles. Firstly it’s important to know the general form of circle,${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ Here the center of the circle is $\left( -g,-f \right)$and the radius of the circle is $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$.When one circle lies completely inside the other without touching, there is no common tangent. The inner circle will have its center lying inside the outer circle when there is not common tangent, which implies that if $\left( {{x}_{1}},{{y}_{1}} \right)$ is a point that lies inside of the circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$, then ${{x}_{1}}^{2}+{{y}_{1}}^{2}+2g{{x}_{1}}+2f{{y}_{1}}+c<0$ . If both the circles touch each other internally then a common point would exist and there would be a possibility of having a common tangent so there shouldn’t exist any common point.

Complete step-by-step answer:
Let us assume that
Here ${{c}_{1}}$and ${{c}_{2}}$ are the centers of the circles ,${{r}_{1}}$and ${{r}_{2}}$ are the respective radii of the circles and Circle-2 lies inside Circle-1:

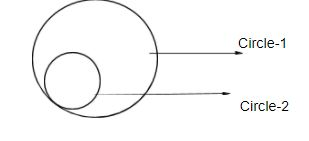
the two equations of circles given are
Circle-1: ${{x}^{2}}+{{y}^{2}}+2ax+c=0$ and Circle-2: ${{x}^{2}}+{{y}^{2}}+2bx+c=0$
For Circle -1: ${{x}^{2}}+{{y}^{2}}+2ax+c=0$
Comparing it with the general form of a circle that is ${{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{f}_{1}}y+{{c}_{1}}=0$
We get

& {{g}_{1}}=a \\\ & {{f}_{_{1}}}=0 \\\ & {{c}_{1}}=c \\\ \end{aligned}$$ $$Center({{C}_{1}})=\left( -{{g}_{1}},-{{f}_{1}} \right)=\left( -a,0 \right)$$ $$Radius({{r}_{1}})=\sqrt{g_{1}^{2}+f_{1}^{2}-{{c}_{1}}}=\sqrt{{{a}^{2}}-c}$$ $${{C}_{1}}=\left( -a,0 \right)$$ and $${{r}_{1}}=\sqrt{{{a}^{2}}-c}$$ For Circle -2: $${{x}^{2}}+{{y}^{2}}+2bx+c=0$$ Comparing it with the general form of a circle that is $${{x}^{2}}+{{y}^{2}}+2{{g}_{2}}x+2{{f}_{2}}y+{{c}_{2}}=0$$ We get $$\begin{aligned} & {{g}_{2}}=b \\\ & {{f}_{2}}=0 \\\ & {{c}_{2}}=c \\\ \end{aligned}$$ $$Center({{C}_{2}})=\left( -{{g}_{2}},-{{f}_{2}} \right)=\left( -b,0 \right)$$ $$Radius({{r}_{2}})=\sqrt{g_{2}^{2}+f_{2}^{2}-{{c}_{2}}}=\sqrt{{{b}^{2}}-c}$$ $${{C}_{2}}=\left( -b,0 \right)$$ and $${{r}_{2}}=\sqrt{{{a}^{2}}-c}$$ Now taking $$x=0$$in both the circles we get Circle-1: $${{y}^{2}}+c=0\to {{y}^{2}}=-c$$ Circle-2: $${{y}^{2}}+c=0\to {{y}^{2}}=-c$$ Now if $$c\le 0$$ then $$y=\sqrt{c}$$ then the point $$\left( 0,\sqrt{c} \right)$$ will be a common point for the both circles and therefore the circles can have a common tangent But our condition is to not a have common tangent Hence $$c>0$$ . Now as Circle-2 lies inside Circle-1 the center of Circle-2 will lie inside Circle-1 It implies that substituting the center of Circle-2 that is $${{C}_{2}}=\left( -b,0 \right)$$ in $${{x}^{2}}+{{y}^{2}}+2ax+c=0$$ $$\begin{aligned} & x=-b,y=0 \\\ & {{\left( -b \right)}^{2}}+{{\left( 0 \right)}^{2}}+2a\left( -b \right)+c<0 \\\ & {{b}^{2}}-2ab+c<0 \\\ & {{b}^{2}}+c<2ab \\\ \end{aligned}$$ We have already derived in the first part of the solution that $$c>0$$ and we know that $${{b}^{2}}>0$$ which says that $${{b}^{2}}+c$$ is always greater than 0 As $$2ab$$ is always greater than $${{b}^{2}}+c$$it implies that $$\begin{aligned} & 2ab>0 \\\ & ab>0 \\\ \end{aligned}$$ So we finally get $$ab>0,c>0$$ Hence option 2 is the correct choice **So, the correct answer is “Option 2”.** **Note:** As the given question the equation of circle is in general form it shouldn’t be mistaken with the standard form. At first we start approaching the solution with the formula for no common tangents which is $${{c}_{1}}{{c}_{2}}<|{{r}_{1}}-{{r}_{2}}|$$but for this question the formula would make the problem a bit lengthier so this alternative solution is preferable.